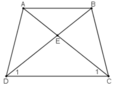
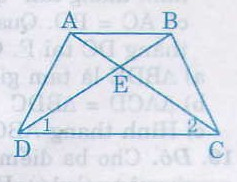
Cho hình thang cân ABCD với đáy nhỏ BC. Gọi E là giao điểm của các đường thẳng AB và CD.
a. Chứng minh rằng EB=EC; EA=ED
b. Gọi P và Q thứ tự là trung điểm của BC và AD. Chứng minh rằng đường thẳng EQ đi qua P và giao điểm hai đường chéo hình thang ABCD

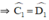
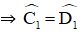
Do ABCD là hình thang cân nên AD = BC, AC = BC, ˆD=ˆCD^=C^
Xét hai tam giác ADC và BCD, ta có: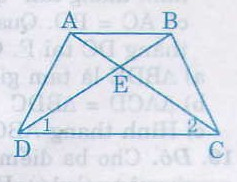
AD = BC (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra ˆC1=ˆD1C1^=D1^
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, ˆD=ˆCD^=C^ , DC là cạnh chung.
bn ơi trả lời sai đề
hok tốt