Cho ▲ABC nhọc đường cao AD, BE và CF cắt nhau tại( D ∈BC;E∈AC; F∈AB). Chứng minh
a. Tam giác ABD đồng dạng tam giác AHF và AF.AB=AH.AD
b.AF.AB=AE.AC và tâm giác AEF đồng dạng Tam giác ABC
c. FC là phân giác của góc EFD và Bc^2=BH.BE+CH.CF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: góc HID+góc HKD=180 độ
=>HIDK nội tiếp
=>góc HIK=góc HDK
=>góc HIK=góc HCB
=>góc HIK=góc HEF
=>EF//IK

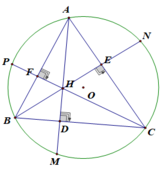
d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠( A 1 ) = ∠( C 2 ) ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠( C 1 ) = ∠( C 2 )
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.

1: AB<AC
=>góc C<góc B
Xét (O) có
góc ACB=1/2*sđ cung AB
góc ABC=1/2*sđ cung AC
mà góc ACB<góc ABC
nên sđ cung AB<sđ cung AC
3: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
4:
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc HFE=góc HBC
=>góc HFE=góc HNM
mà hai góc này ở vị trí đồng vị
nên FE//MN

xét tứ giác BFHD có
góc BFH + góc BDH = 180
mà nó là 2 góc đối => nội tiếp => góc FDH = góc FBE
chứng minh tương tự với tứ giác CEHD
=> góc HDE = góc HCE
Xét tứ giác BFEC có
góc BFC = góc BEF = 90
mà nó là 2 góc kề => tứ giác nội tiếp
mà góc BEC = 1/2 sđ BC = 90 => SĐ BC = 180 => BC là đường kính mà I là trung điểm BC => I là tâm đường tròn ngoại tiếp tứ giác BFEC
=> góc FIE = góc FBE + góc FCE
=> Góc FIE = góc FDH+góc HDE => góc FIE = góc FDE
mà nó là 2 góc kề => nội tiếp
=> điều phải cm

-Xét △BCF và △BAD có:
\(\widehat{ABC}\) là góc chung
\(\widehat{BFC}=\widehat{BDA}=90^0\)
\(\Rightarrow\)△BCF∼△BAD (g-g).
\(\Rightarrow\dfrac{BC}{BA}=\dfrac{BF}{BD}\) (tỉ số đồng dạng)
\(\Rightarrow BF.BA=BC.BD\left(1\right)\)
-Xét △ACD và △BCE có:
\(\widehat{ACB}\) là góc chung
\(\widehat{ADC}=\widehat{BEC}=90^0\)
\(\Rightarrow\)△ACD∼△BCE (g-g)
\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CD}{CE}\) (tỉ số đồng dạng)
\(\Rightarrow CE.CA=CD.BC\left(2\right)\)
-Từ (1) và (2) suy ra:
\(BF.BA+CE.CA=BD.BC+CD.BC=BC\left(BD+CD\right)=BC.BC=BC^2\)
a) xét tam giác ABD và tam giác AHF có
góc BAD chung
Góc AFH = góc ADB (=90 độ)
=> tam giác ABD đồng dạng vs tam giác AHF (g.g)
=> AB/AD = AH/AF
=> AF.AD = AH.AD
b) xét tam giác AFC và tam giác AEB có
Góc A chung
Góc AFC = góc AEB (=90 độ)
=> tam giác AFC đồng vs tam giác AEB (g.g)
=> AF/AC = AE/AB
=> AF.AB= AE.AC
a: Xét ΔABD vuông tại D và ΔAHF vuông tại F có
góc FAH chung
=>ΔABD đồng dạng với ΔAHF
=>AB/AH=AD/AF
=>AB*AF=AH*AD
b: Xet ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
c:góc FEC=góc DAC
góc DFC=góc EBC
mà góc DAC=góc EBC
nên góc FEC=goc DFC
=>FC là phân giác của góc EFD