Cho ΔABC và tam giác có ba đỉnh D; E; F biết AB = EF, B=F. Cần thêm điều kiện gì để hai
tam giác bằng nhau theo trường hợp góc – cạnh – góc
A. AC = FD B. A=F C. C=E D. A=E
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=căn 10^2-5^2=5*căn 3(cm)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
c: Sửa đề: ΔBEF=ΔBAC
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc FBE chung
=>ΔBEF=ΔBAC

a: \(AC=\sqrt{BC^2-AB^2}=5\sqrt{3}\left(cm\right)\)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
=>BD là đường trung trực của AE
hay BD\(\perp\)AE

Ta có: ∠B =∠K nên đỉnh B tương ứng với đỉnh K
AB = KD nên đỉnh A tương ứng với đỉnh D
Suy ra đỉnh C tương ứng với đỉnh H
Vậy ΔABC=ΔDKH

Vì ∠A =∠F nên đỉnh A tương ứng với đỉnh F
Vì ∠B =∠E nên đỉnh B tương ứng với đỉnh E
Suy ra đỉnh C tương ứng với đỉnh D
Vậy ΔABC=ΔFED

Ta có: AB = ED và AC = FD nên đỉnh A tương ứng với đỉnh D, đỉnh B tương ứng đỉnh E, đỉnh C tương ứng với F.
Vậy ΔABC=ΔDEF

HD: Chọn ra 3 đỉnh bất kỳ của đa giác có: C 10 3 cách chọn.
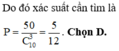
■ Số tam giác có 2 cạnh là cạnh của đa giác là: 10
(vì ứng với mỗi đỉnh ta lấy 2 cạnh kề với nó là được tgiác như điều kiện đã xét)
■ Số tam giác có 1 cạnh là cạnh của đa giác là: 10.6 = 60 vì chọn 1 cạnh của đa giác, ta chọn được 6 đỉnh để tạo tam giác (trừ đi 2 đỉnh của cạnh đó và 2 đỉnh nằm kề sát cạnh đó), mà có 10 cạnh như thế nên có 10.6 = 60
Suy ra số tgiác được tạo thành từ các đường chéo của đa giác là: 120 - 10 - 60 = 50 tam giác.
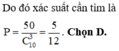
Chọn B