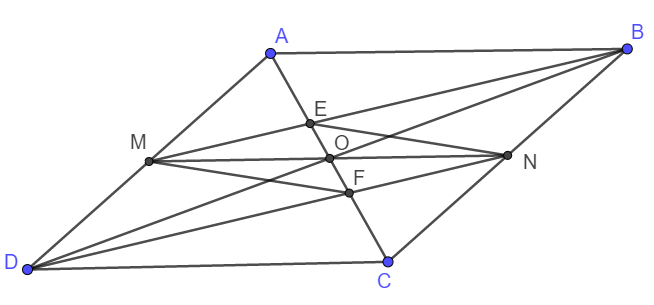
a) Do ABCD là hình bình hành nên AD song song và bằng BC.

Lại có M, N là trung điểm AD, BC nên DM song song và bằng BN. Suy ra DMBN là hình bình hành, hay MB//DN.

Xét tam giác ADF, có:

M là trung điểm AC

ME//DF

\(\Rightarrow\) ME là đường trung bình tam giác ADF.

Vậy AE =  EF.

Hoàn toàn tương tự : EF = FC.

Vậy nên AE = EF = FC.

b) DMBN là hình bình hành nên hai đường chéo DB và MN cắt nhau tại trung điểm mỗi đường.

Vậy thì O là trung điểm MN.

Lại có: AO = OC; AE = FC nên AO - AE = OC - FC hay EO = OF.

Xét tứ giác MENF có O là trung điểm hai đường chéo EF và MN nên MENF là hình bình hành.

c) 

+) Để hình bình hành MENF là hình chữ nhật thì hai đường chéo MN và EF bằng nhau.

Lại có MN = AB, EF = \(\frac{AC}{3}\). Vậy hình bình hành ABCD phải có đường chéo AC = 2AB thì MENF là hình chữ nhật.

+) Để hình bình hành MENF là hình thoi thì hai đường chéo MN và EF phải vuông góc.

Vậy thì \(EF\perp MN\Rightarrow AC\perp AB\)

Vậy hình bình hành ABCD phải có đường chéo AC vuông góc với cạnh AB thì MENF là hình thoi.

+) Để hình bình hành MENF là hình vuông thì nó vừa là hình chữ nhật, vừa là hình thoi.

Vậy thì hình bình hành ABCD có đường chéo AC vuông góc với AB và AC = 2AB.

b)có AM=MC (định lý đường trug tuyến tg vuông)

suy ra tg AMC cân tại M. gọi MN cắt AC tại O

mà MO là đg cao( AO vuông góc vs AC)

suy ra MO là trug tuyến (trog tg vuông 1 đg đóng vtro các đg còn lại) suy ra AO=OC

xét tứ giác MANC có:  MO=NO; AO=OC suy ra tứ giác này là hình bình hành

có MN vuông góc vsAC suy ra tứ giác này là hình thoj(dấu hiệu nhận biết)

c) có AM=MB (đg trug tyến tg vuông) suy ra tg AMB cân tại M

suy ra BE=AE(1 đg đóng vtro các đg còn lại)

suy ra EA=3cm

có AF=FC( t'c hình thoi)

suy ra  AF=4cm

S hình chữ nhật EMFA là;

3 nhân 4 +12(cm²⁾

xin lỗi mik mới học lớp 6 à

Gọi I là trung điểm của AB.

Giả sử đường thẳng IE cắt CD tại K₁ 

Có: \(\frac{IA}{K_1D}=\frac{EI}{EK_1}=\frac{IB}{K_1C}\) (hệ quả định lý Ta lét)

mà IA = IB (gt) nên K₁D = K₁C, do đó K₁ là trung điểm CD

Giả sử đường thẳng IF cắt CD tại K₂

Có: \(\frac{IA}{K_2C}=\frac{FI}{FK_2}=\frac{IB}{K_2D}\) (hệ quả định lý Ta lét)

mà IA = IB (gt) nên K₂C = K₂D, do đó K₂ là trung điểm CD 

do IE và IF cùng đi qua trung điểm K của CD nên hai đường thẳng này trùng nhau

Vậy ta có đpcm

Bạn ơi gọi luôn I là trung điểm AB thì sai r