Cho tam giác ABC vuông tại A (AB < AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)
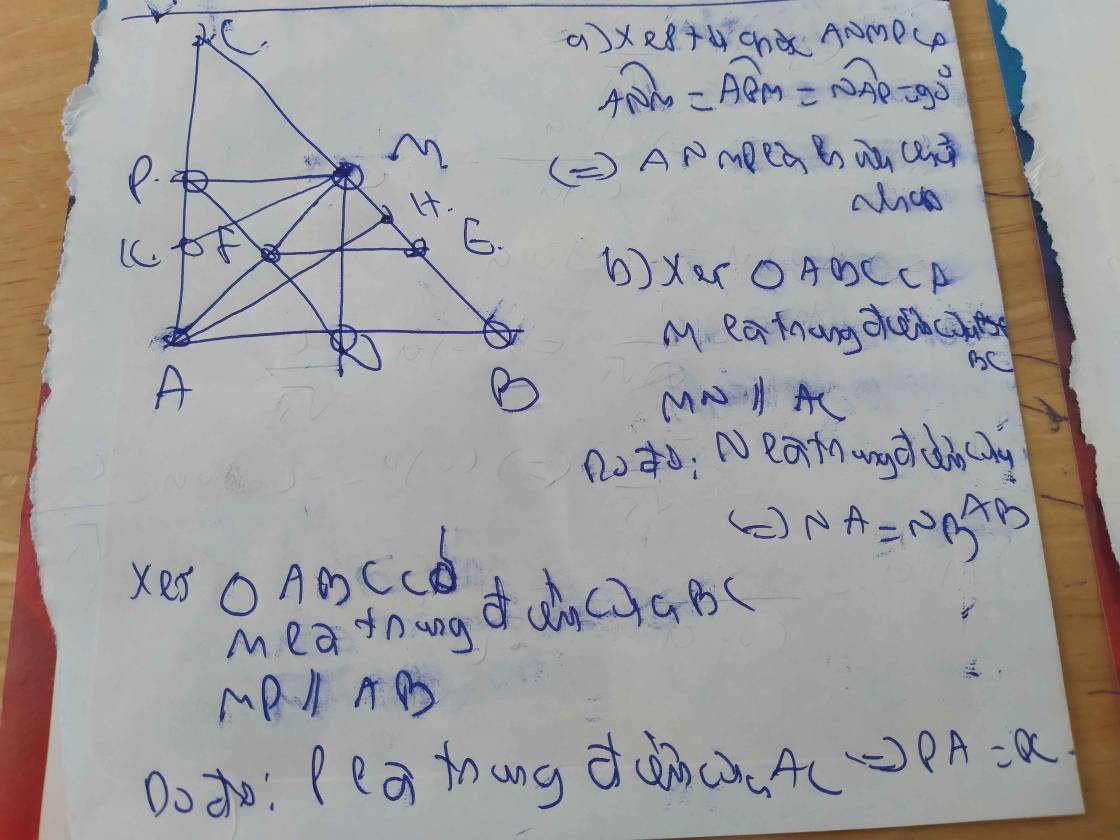
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA=NB, PA=PC và tứ giác BMPN là hình bình hành
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh
+ Tứ giác ABEF là hình thang cân
+ Tứ giác MENF là hình thoi
Giúp câu c với cac bn ơi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2023
a: Xét tứ giác ANMP có
\(\widehat{ANM}=\widehat{APM}=\widehat{NAP}=90^0\)
=>ANMP là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
MN//AC
Do đó: N là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MP//AB
Do đó: P là trung điểm của AC
Xét ΔABC có
N,P lần lượt là trung điểm của AB,AC
=>NP là đường trung bình của ΔABC
=>NP//BC và NP=BC/2
=>NP//MH
Ta có: ΔHAC vuông tại H
mà HP là đường trung tuyến
nên HP=AP
mà AP=MN(ANMP là hình chữ nhật)
nên HP=MN
Xét tứ giác MHNP có MH//NP
nên MHNP là hình thang
Hình thang MHNP có MN=HP
nên MHNP là hình thang cân
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
24 tháng 8 2023
a/
\(MP\perp AC;NA\perp AC\) => MP//NA
\(MN\perp AB;PA\perp AB\) => MN//PA
=> ANMP là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có \(\widehat{A}=90^o\)
=> ANMP là hình chữ nhật (hbh có 1 góc vuông là HCN)
b/
MN//PA (cmt) => MN//AC
MB=MC (gt)
=> NA=NB (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
C/m tương tự cũng có PA=PC
Ta có
MP//NA (cmt) => MP//NB
NA=NB; PA=PC => NP là đường trung bình của tg ABC
=> NP//BC => NP//MB
=> BMPN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Xét HCN ANMP có
FM=FA (trong HCN 2 đường chéo cắt nhau tại trung điểm mỗi đường)
EM=EB (gt)
=> EF là đường trung bình của tg MAB => EF//AB
=> ABEF là hình thang
Ta có
MB=MC => AM=MB=MC=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Ta có
FM=FA=AM/2
EB=EM=BM/2
=> FA=EB
=> ABEF là hình thang cân
d/
6 tháng 12 2021
Ta có: MN ⊥ AB
=> góc MNA = 900
MP ⊥ AC
=> góc MPA = 900
Xét tứ giác ANMP có:
góc MNA = góc MPA = góc NAP = 900
=> tứ giác ANMP là hình vuông
Kéo dài MN cắt AB tại D => CA; MD là đường cao tg CBD => K là trực tâm=> BK _|_CD (1*)
Mà AH//MD \(\Rightarrow\) \(\frac{BA}{BD}=\frac{BH}{BM}\Rightarrow\frac{2BN}{BD}=\frac{BH}{BM}\Rightarrow\frac{BN}{BD}=\frac{BH}{2BM}=\frac{BH}{BC}\Rightarrow\)NH//CD (2*)
Từ (1*,2*) => BK _|_HN\(\Rightarrowđcpm\)
bÀI LÀM
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)