Cho hai da thuc
F(x)=X3+x-1; Q(x)=3x-x2+x3+1
Tinh F(x)+Q(x)
F(x)-Q(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
0
D
8 tháng 5 2016
a)
xét f(x)=0
=>3x-6=0
=> 3x=6
=> x=2
vậy nghiệm của f(x) là 2
xét g(t)=0
=> -4t-8=0
=> -4t=8
=> t=-2
vậy nghiệm của g(t) là -2
b)
f(x)=1=> 3x-6=1
=> 3x=7
=> x=7/3
g(t)=1=> -4t-8=1
=> -4t=9
=> t=-9/4
1 tháng 5 2022
a)
xét f(x)=0
=>3x-6=0
=> 3x=6
=> x=2
vậy nghiệm của f(x) là 2
xét g(t)=0
=> -4t-8=0
=> -4t=8
=> t=-2
vậy nghiệm của g(t) là -2
b)
f(x)=1=> 3x-6=1
=> 3x=7
=> x=7/3
g(t)=1=> -4t-8=1
=> -4t=9
=> t=-9/4
TM
0
G
28 tháng 8 2017
Giải:
a) \(\left(x^2+2x+1\right)\left(x+1\right)\)
\(=x^2.x+2x.x+1.x+x^2.1+2x.1+1.1\)
\(=x^3+2x^2+x+x^2+2x+1\)
\(=x^3+3x^2+3x+1\)
b) \(\left(x^3-x^2+2x-1\right)\left(5-x\right)\)
\(=x^3.5-x^2.5+2x.5-1.5+x^3.\left(-x\right)-x^2.\left(-x\right)+2x.\left(-x\right)-1.\left(-x\right)\)
\(=5x^3-5x^2+10x-5-x^4+x^3-2x^2+x\)
\(=6x^3-7x^2+11x-5-x^4\)
c) \(\left(x-5\right)\left(x^3-x^2+2x-1\right)\)
\(=x.x^3-5.x^3+x.\left(-x^2\right)-5.\left(-x^2\right)+x.2x-5.2x+x.\left(-1\right)-5.\left(-1\right)\)
\(=x^4-5x^3-x^3+5x^2+2x^2-10x-x+5\)
\(=x^4-6x^3+7x^2-11x+5\)
Chúc bạn học tốt!!!
12 tháng 9 2017
lớp 8 Phạm Hoàng Giang không chơi kiểu lớp 7
đúng làm 8 mà làm
\(A=\left(x^2+2x+1\right)\left(x+1\right)=\left(x+1\right)^2\left(x+1\right)=\left(x+1\right)^3\)
\(A=x^3+3x^2+3x+1\)
TM
2
10 tháng 1 2021
Rõ ràng đa thức \(x^3-1\) chia hết cho đa thức \(x^2+x+1\).
Ta tách: \(x^9+x^6+x^3+1=\left(x^9-1\right)+\left(x^6-1\right)+\left(x^3-1\right)+4=\left(x^3-1\right)\left(x^6+x^3+1\right)+\left(x^3-1\right)\left(x^3+1\right)+\left(x^3-1\right)+4\).
Từ đây suy ra đa thức đó chia cho đa thức \(x^2+x+1\) được đa thức dư là 4.
20 tháng 7 2021
a) Đặt A(x)=0
\(\Leftrightarrow-4x-5=0\)
\(\Leftrightarrow-4x=5\)
hay \(x=-\dfrac{5}{4}\)
b) Đặt B(x)=0
\(\Leftrightarrow3\left(2x-1\right)-2\left(x+1\right)=0\)
\(\Leftrightarrow6x-3-2x-2=0\)
\(\Leftrightarrow4x=5\)
hay \(x=\dfrac{5}{4}\)
CM
19 tháng 4 2017
Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
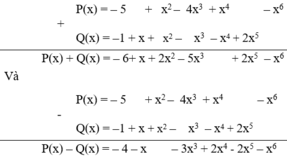
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6
22 tháng 6 2023
a: f(0)=0+0-0+3=3
=>x=0 ko là nghiệm của f(x)
g(0)=0+0+0+1=1
=>x=0 ko là nghiệm của g(x)
b: f(x)+g(x)
=x^3+4x^2-5x+3+x^3+3x^2-2x+1
=2x^3+7x^2-7x+4
c: f(x)-g(x)
=x^3+4x^2-5x+3-x^3-3x^2+2x-1
=x^2-3x+2
AH
Akai Haruma
Giáo viên
16 tháng 5 2021
Lời giải:
$P(x)+Q(x)=-x^3+2x^2+x-1+x^3-x^2-x+2$
$=x^2+1\geq 0+1>0$ với mọi $x\in\mathbb{R}$
Do đó đa thức $P(x)+Q(x)$ vô nghiệm.
F(x)+Q(x) = 2x^3 +4x -x^2
F(x) - Q(x) = -2x +x^2 -2