Bài 1; pttnt
b) 25(x-y)^2-16(x+y)^2
Bài 2; cho biểu thức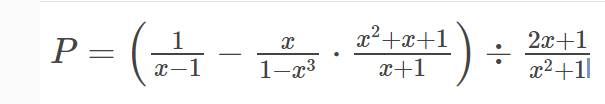
a) Tìm điều kiện xác định của P
b) rút gọn biểu thức P
c) tính giá trị của P khi x=1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 2 2017
Số em làm được cả 3 bài là: 1 em
Số em làm được bài 1 và 2 mà không làm được bài 3 còn lại là
2-1=1( em)
Số em làm được bài 1 và bài 3 mà không làm được bài 2 là:
6-1=5( em)
Số em làm được bài 2 và 3 mà không làm được bài 1 là
5-1=4( em)
Số em chỉ làm được bài 1 là
20-1-1-5=13( em)
Số em chỉ làm được bài 2 là:
14-1-1-4=8( em)
Số em chỉ làm được bài 3 là
10-1-4-5= 0( em)
Tổng số hs của lớp là
1+1+5+4+13+8= 32( em)
9 tháng 6 2021
Số em làm được cả 3 bài là: 1 em Số em làm được bài 1 và 2 mà không làm được bài 3 còn lại là 2-1=1( em) Số em làm được bài 1 và bài 3 mà không làm được bài 2 là: 6-1=5( em) Số em làm được bài 2 và 3 mà không làm được bài 1 là 5-1=4( em) Số em chỉ làm được bài 1 là 20-1-1-5=13( em) Số em chỉ làm được bài 2 là: 14-1-1-4=8( em) Số em chỉ làm được bài 3 là 10-1-4-5= 0( em) Tổng số hs của lớp là 1+1+5+4+13+8= 32( em)
CM
10 tháng 1 2017
Số em làm được cả 3 bài là: 1 em Số em làm được bài 1 và 2 mà không làm được bài 3 còn lại là 2-1=1( em) Số em làm được bài 1 và bài 3 mà không làm được bài 2 là: 6-1=5( em) Số em làm được bài 2 và 3 mà không làm được bài 1 là 5-1=4( em) Số em chỉ làm được bài 1 là 20-1-1-5=13( em) Số em chỉ làm được bài 2 là: 14-1-1-4=8( em) Số em chỉ làm được bài 3 là 10-1-4-5= 0( em) Tổng số hs của lớp là 1+1+5+4+13+8= 32( em)
2T
2
17 tháng 12 2021
Bài 1:
\(a,ĐK:x+5\ge0\Leftrightarrow x\ge-5\\ b,ĐK:\dfrac{2021}{4-2x}\ge0\Leftrightarrow4-2x>0\Leftrightarrow x< 2\)
Bài 2:
\(a,=5\sqrt{3}-4\sqrt{3}-10\sqrt{3}-3\sqrt{3}=-12\sqrt{3}\\ b,=2\sqrt{5}+\dfrac{8\left(3-\sqrt{5}\right)}{4}=2\sqrt{5}+6-2\sqrt{5}=6\)
Bài 3:
\(A=\dfrac{\sqrt{x}-2+2\sqrt{x}+4+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3}{\sqrt{x}-2}\)
Bài 4:
\(a,\Leftrightarrow\left|3x-2\right|=7\Leftrightarrow\left[{}\begin{matrix}3x=9\\3x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{3}\end{matrix}\right.\\ b,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow5\sqrt{2x-1}-\sqrt{2x-1}=12\\ \Leftrightarrow\sqrt{2x-1}=3\Leftrightarrow2x-1=9\\ \Leftrightarrow x=5\left(tm\right)\)
Bài 5:
\(b,\Leftrightarrow\left\{{}\begin{matrix}m-1=2\\2m+\sqrt{5}\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne\dfrac{-3-\sqrt{5}}{2}\end{matrix}\right.\Leftrightarrow m=3\)
DT
17 tháng 12 2021
1,
a, x khác phân số có mẫu là 0
b,x khác 2
4,
a, theo đề:
=>(3x-2)^2=49
=>3x-2=7
x=3
bt cs nhiu đây à :<
Câu 1:
\(25\left(x-y\right)^2-16\left(x+y\right)^2\)
\(=\left[5\left(x-y\right)\right]^2-\left[4\left(x+y\right)\right]^2\)
\(=\left(5x-5y\right)^2-\left(4x+4y\right)^2\)
\(=\left(5x-5y-4x-4y\right)\left(5x-5y+4x+4y\right)\)
\(=\left(x-9y\right)\left(9x-y\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{1;-\dfrac{1}{2}\right\}\)
b: \(P=\left(\dfrac{1}{x-1}-\dfrac{x}{1-x^3}\cdot\dfrac{x^2+x+1}{x+1}\right):\dfrac{2x+1}{x^2+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{x+1}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\dfrac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^2+1}{2x+1}=\dfrac{x^2+1}{x^2-1}\)
c: Thay x=1/2 vào P, ta được:
\(P=\dfrac{\left(\dfrac{1}{2}\right)^2+1}{\left(\dfrac{1}{2}\right)^2-1}=\dfrac{5}{4}:\dfrac{-3}{4}=\dfrac{5}{4}\cdot\dfrac{-4}{3}=-\dfrac{5}{3}\)