Chọn C

+ Bước sóng của sóng  λ = v 2 π ω =   3 , 5   c m

Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:

  - A B λ ≤ k ≤ A B λ ⇔   - 5 , 7 ≤ k ≤ 5 , 7

Vậy có 11 điểm

- Bước sóng của sóng:

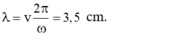
- Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:

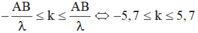
- Vậy có 11 điểm

$\lambda = \dfrac{3}{2}$

Vị trí cực đại thoả mãn: $(20-20\sqrt {2} \le (k+0,5)\lambda \le 20 \Rightarrow $ số $k=19$ 

Vậy có 19 điểm dao động biên độ cực đại trên đoạn AD.

Đáp án B

+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì:

d 1 - d 2 = ( k + 1 2 ) λ

+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số d₁ – d₂:

AM - 2 AM ≤ d 1 - d 2 ≤ AB

+ Kết hợp hai phương trình trên ta thu được:

AM ( 1 - 2 ) λ - 1 2 ≤ k ≤ A B λ - 1 2

→ - 6 , 02 ≤ k ≤ 12 , 8

Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.

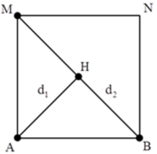
Đáp án B

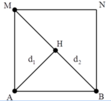
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì:

d 1 - d 2 = k + 1 2 λ

+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số  d 1 - d 2 : A M - 2 A M ≤ d 1 - d 2 ≤ A B

+ Kết hợp hai phương trình trên ta thu được: A M 1 - 2 λ - 1 2 ≤ k ≤ A B λ - 1 2

→ - 6 , 02 ≤ k ≤ 12 , 8

Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM

Đáp án A

Bước sóng λ = v/f = 30/20 = 1,5 cm

+ Số điểm dao động với biên độ cực đại trên đoạn BM là số giá trị nguyên của k thỏa mãn:

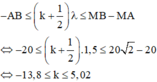
→ Có 19 điểm

<Em ko bt có đề là như thế hay là mình chép lộn không nhưng đây là cách làm tìm "Số điểm dao động với biên độ cực đại trên đoạn BM " Chị tham thảo nha.>

THAM THẢO

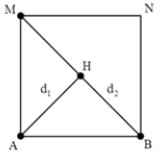
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì

 \(d_1-d_2=\left(k+\dfrac{1}{2}\right)\lambda\)

+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số

\(\dfrac{d_1-d_2}{AM-\sqrt{2}AM}\le d_1-d_2\le AB\)

+ Kết hợp hai phương trình trên ta thu được

\(\dfrac{\left(k+\dfrac{1}{2}\right)\lambda}{AM-\sqrt{2}AM}\le\left(k+\dfrac{1}{2}\right)\lambda\le AB\)

\(\Leftrightarrow\dfrac{AM\left(1-\sqrt{2}\right)}{\lambda}-\dfrac{1}{2}\le k\le\dfrac{AB}{\lambda}-\dfrac{1}{2}\)

\(\Rightarrow-6,02\le k\le12,8\)

Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.

Đáp án C

+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì

d 1 - d 2 = ( k + 1 2 ) λ

+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số

+ Kết hợp hai phương trình trên ta thu được

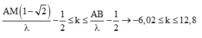
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM

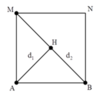
Đáp án C

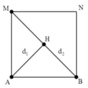
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì: d 1 - d 2 = k + 1 2 λ

+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số  d 1 - d 2 : A M - 2 A M ≤ d 1 - d 2 ≤ A B

+ Kết hợp hai phương trình trên ta thu được

A M 1 - 2 λ - 1 2 ≤ k ≤ A B λ - 1 2

→ - 6 , 02 ≤ k ≤ 12 , 8

Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.