Cho hình vuông ABCD có M;N là trung điểm của BC;CD.tìm đỉnh B biết điểm N (0;-2) và AM có pt :x+2y-2=0 và cạnh hình vuông bằng 4
m.n giúp mk với ; các cậu thử giải tìm xem có bao nhiêu điểm M nhé thank nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

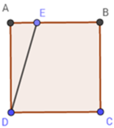
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

a: CD vuông góc DA
CD vuông góc SA
=>CD vuông góc (SAD)
=>CD vuông góc SD
b: CD vuông góc AK
AK vuông góc SD
=>AK vuông góc (SCD)
=>SC vuông góc AK
BC vuông góc AH
AH vuông góc SB
=>AH vuông góc SC
=>SC vuông góc (AKH)
c: (SO;(ABCD))=(OS;OA)=góc SOA

1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)