Tìm tập nghiệm S của bất phương trình 1 3 x + 1 - 3 > 0
A. S = - ∞ ; - 2
B. S = - 1 ; + ∞
C. S = 1 ; + ∞
D. S = - 2 ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .

Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
![]()
Khi đó, bất phương trình
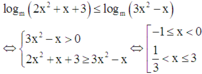

Đáp án D
B P T ⇔ 3 3 x 2 − 10 10 x + 3 ≤ 0 ⇔ 1 3 ≤ 3 x ≤ 3 ⇔ − 1 ≤ x ≤ 1 ⇒ ⇒ T = 2.
Đáp án A
3 - x - 1 > 3 1 → 3 > 1 - x - 1 > 1 ⇔ x < - 2