40. HS y = cosx đồng biến trên khoảng nào sau đây
A. ( π/2;π)
B. (0;π)
C. (0;π/2)
D. (-π/2;0)
41. HS y = tanx đồng biến trên khoảng nào sau đât
A. (π/2;2π)
B. (0;π)
C. (-π;0)
D. (-π/2;π/2)
42. HS y = cotx nghịch biến trên khoảng nào sau đây
A. (0;2π)
B. (0;π)
C. (-π;π)
D. (-π/2;π/2)
43. Đồ thị hàm số y= cosx đi qua điểm nào sau đây
A. M(π;1)
B. N(0;1)
C. P (-1;π)
D. Q(3π;1)

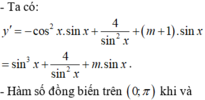
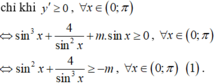
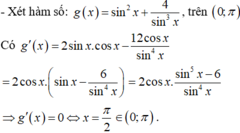
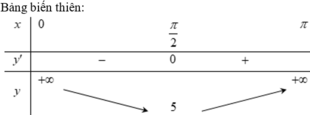


Câu 40: D
Câu 41: D
Câu 42: B
Câu 43: B