Cho 3 điểm A(0:2) , B(2;4) , C (-1;1)
a, Lập pt đg thẳng AB
b, Chứng minh ABC thẳng hàng
c, Xác định m để dths y =(2m2-m)x +m2+m là một dg thẳng song song vs AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các điểm nằm trên trục hoành là các điểm có tung độ bằng 0. Trong số các điểm ở trên ta thấy những điểm có tung độ bằng 0 là: A(-1; 0), D(3; 0), O(0; 0) . Vậy có ba điểm nằm trên trục hoành
Chọn đáp án D

Gọi d: y = ax + b là đường thẳng đi qua A và B
A ( 0 ; 3 ) ∈ ( d ) ⇔ a . 0 + b = 3 ⇔ b = 3 B ( 2 ; 2 ) ∈ ( d ) ⇔ a . 2 + b = 2 ⇒ b = 3 2 a + b = 2 ⇔ b = 3 a = − 1 2 ⇒ d : y = − 1 2 x + 3
Để 2 điểm A, B, C thẳng hàng thì C ( m + 3 ; m ) ∈ ( d ) y = − 1 2 x + 3
⇔ m = − 1 2 ( m + 3 ) + 3 ⇔ 3 2 m = 3 2 ⇒ m = 1
Vậy m = 1
Đáp án cần chọn là: A

\(a,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)
Ta có \(\left(d\right)\) đi qua \(A\left(-3;0\right),B\left(0;2\right)\) nên \(\left\{{}\begin{matrix}0=-3a+b\\2=0a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=2\end{matrix}\right.\)
Vậy đths là \(\left(d\right):y=\dfrac{2}{3}x+2\)
\(b,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)
Ta có hệ pt \(\left\{{}\begin{matrix}1=0a+b\\0=-a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
Vậy đths là \(\left(d\right):y=x+1\)
a,a, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b
Ta có (d)(d) đi qua A(−3;0),B(0;2)A(−3;0),B(0;2) nên {0=−3a+b2=0a+b⇔⎧⎨⎩a=23b=2{0=−3a+b2=0a+b⇔{a=23b=2
Vậy đths là (d):y=23x+2(d):y=23x+2
b,b, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b
Ta có hệ pt {

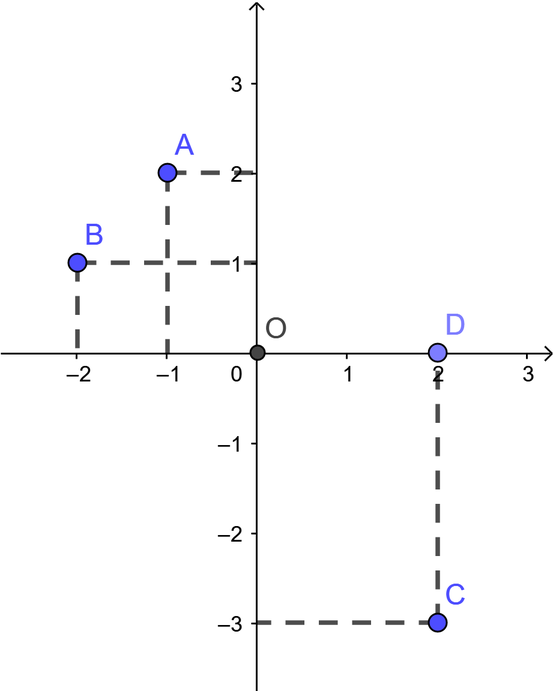
Biểu diễn các điểm trên hệ trục tọa độ Oxy ta thấy có hai điểm nằm trong góc phần tư thứ hai là A và B
Chọn đáp án C

Ta có:
a) Điểm -5 nằm bên trái điểm -3, nên -5 nhỏ hơn -3, và viết: -5 < -3
b) Điểm 2 nằm bên phải điểm -3, nên 2 lớn hơn -3, và viết 2 > -3
c) Điểm -2 nằm bên trái điểm 0, nên -2 nhỏ hơn 0, và viết -2 < 0

Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.

Có: `x-2y+4=0`
`<=>x=2y-4`
Thay `x=2y-4` vào `(E)` có:
`3(2y-4)^2+4y^2-48=0`
`<=>3(4y^2-16y+16)+4y^2-48=0`
`<=>12y^2-48y+48+4y^2-48=0`
`<=>` $\left[\begin{matrix} y=3\\ y=0\end{matrix}\right.$
`@y=3=>x=2.3-4=2`
`@y=0=>x=2.0-4=-4`
`=>` Tọa độ giao điểm của `(E)` và `(d)` là: `(2;3)` và `(-4;0)`
`->D`
\(\Rightarrow\) \(chọn\) \(D\)
\(xét\) \(hpt\) \(:\)
\(\left\{{}\begin{matrix}3x^2+4y^2-48=0\\x-2y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(2y-4\right)^2+4y^2-48=0\\x=2y-4\end{matrix}\right.\)
\(giải:\) \(3\left(4y^2-16y+16\right)+4y^2-48=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}12y^2-48y+48+4y^2-48=0\\16y^2-48y=0\\\left[{}\begin{matrix}y=0\Rightarrow x=-4\\y=3\Rightarrow x=2\end{matrix}\right.\end{matrix}\right.\)
\(vậy\) \(giao\) \(điểm\) \(của\) \(elip\) \(\left(E\right)\) \(là\) \(\left(-4;0\right)\) \(và\) \(\left(2;3\right)\)

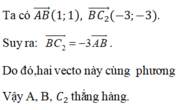
a) Gọi phương trình đường thẳng AB có dạng d: y=ax+b , a khác 0
A thuộc d=>2=a.0+b
B thuộc d => 4=2.a+b
=> b=2, a=1
AB: y=x+2
b) Để chứng minh ABC thẳng hàng em chứng minh C thuộc dường thẳng AB
Vì 1=-1+2 => C thuộc AB
c) Song song
2m^2-m=a=1
m^2+m khác 2
Em giải ra nhé