Bài 1: Tìm số hạng thứ 4 lập thành 1 tỉ lệ thức (TLT) với 3 số hạng sau: 4;25;100
Bài 2: Cho TLT \(\frac{3x+5y}{x-2y}=\frac{1}{4}.\)Tính tỉ số \(\frac{x}{y}\)
Bài 3: Cho TLT \(\frac{a-3}{a+3}=\frac{b-6}{b+6}\) với a \(\ne\) 3; b \(\ne\)–6. CMR: \(\frac{a}{b}=\frac{1}{2}\)
Bài 4: Các số a,b,c phải có thêm điều kiện gì để có TLT:
\(\frac{a}{b}=\frac{a+c}{b+c}\)với b \(\ne\)0; b + c \(\ne\)0.
Bài 5: Cho TLT \(\frac{a^2+b^2}{b^2+c^2}=\frac{a}{c}\) với a,b,c \(\ne\)0; a \(\ne\)c. CMR: \(\frac{ab}{bc}=\frac{b}{c}\)
Bài 6: Tìm các số x,y,z biết:
a, \(\frac{x}{y}=\frac{8}{11};\frac{y}{z}=\frac{11}{7}\) và x + y - 10z = – 102
b, 9x = 5y = 15z và –x + y - z = 11
c, \(\frac{3}{7}x=\frac{8}{13}y=\frac{6}{19}z\) và 2x - y - z = – 6
Bài 8: Cho TLT . Chứng minh:
a, \(\frac{a-b}{a+b}=\frac{c-d}{c+d}\) b, \(\frac{a-b}{c-d}=\frac{2a-3b}{2c-3d}\) c, \(\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\)

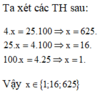
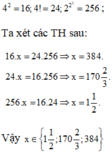
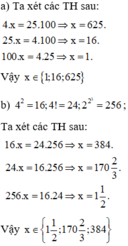
2. \(\frac{\left(3X+5Y\right)}{X-2Y}=\frac{1}{4}=>4\left(3X+5Y\right)=X-2Y\\ 12X+20Y=X-2Y\\ X-12X=2Y-20Y\\ -11X=-18Y\\ =>\frac{X}{Y}=-\frac{18}{-11}=\frac{18}{11}\)
Bài 1. 4/25 = 100/x => x = 25.100/4 = 2500/4 = 625
Bài 3. (a-3)/(a+3) = (b-6)/(b+6)
=> (a-3)(b+6) = (a+3)(b-6)
=> ab + 6a -3b -18 = ab - 6a + 3b -18
=> 12a = 6b
=> a/b = 6/12 = 1/2