Cho Parabol (P) có đỉnh ở gốc tọa độ và đi qua điểm A(-3;3).
1. Viết phương trình của Parabol (P).
2. Viết phương trình đường thẳng (d) song song với đường thẳng (d’): y = x – 2017 và đi qua điểm B(0;1-n). Xác định n sao cho đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoành độ x1;x2 thỏa mãn: |x1 - x2| = \(\sqrt{5}\)




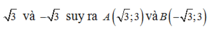

1: Thay x=-3 và y=3 vào (P),ta được:
\(a\cdot\left(-3\right)^2=3\)
=>9a=3
hay a=1/3