Cho hàm số y=f(x) xác định và liên tục trên đoạn [-1;3] có đồ thị như hình vẽ sau.
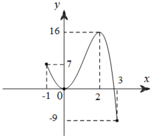
Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y = |f(x)+m| trên đoạn [-1;3] bằng 2018?
A. 2.
B. 4.
C. 6
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Quan sát đồ thị hàm số, ta thấy có hai điểm cực đại thuộc đoạn [-2; 3]

Đáp án là B.
Từ đồ thị của hàm số y , = f ( x ) ta có bảng biến thiên của hàm số y = f ( x ) như hình vẽ:

Từ bảng biến thiên ta có: M = m a x { f ( - 1 ) ; f ( 1 ) ; f ( 2 ) }

Đáp án A
Từ bảng biến thiên của hàm số y=f(x), suy ra bảng biến thiên của hàm số y = f ( x ) là
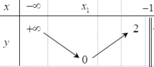

Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.

Qua điểm x = 0 đạo hàm không đổi dấu nên không thể là điểm cực trị của hàm số.
Chọn đáp án D.

Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.
Đáp án A.