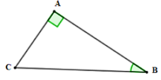
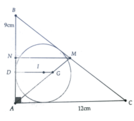
cho tam giác ABC vuông tại A,có AB=12 cm ;AC=16 cm kẻ đường cao AH (H thuộc BC)
chứng minh tam giác HBA đồng dạng với tam giác ABC
tính độ dài các cạnh BC,AH
trên tia HC lấy điểm D sao cho HD=HA.Đường vuông góc với BC tại D cắt AC tại E .Gọi M là trung điểm của BE,tia AM cắt BC tại G. chứng minh GB trên BC =HD trên AH+HC