30cm2

dc=7hay5

Kẻ DH ^ AB tại H

⇒ A H = A D 2 = 4 c m  

Áp dụng định lý Pytago trong D vuông ADH Þ DH = 4 3 cm.

ÞS_ABCD = DH.AB = 120cm²

Độ dài đoạn thẳng DC là:

\(12+5=17\left(cm\right)\)

Diện tích hình bình hành ABCD là:

\(17\text{×}8=136\left(cm^2\right)\)

Đáp số: ...

\(S_{ABCD}=AB\cdot DH=8\cdot\left(30-10\right)=8\cdot20=160\left(cm^2\right)\)

Vẽ đường cao AH của hình bình hành ABCD (H thuộc CD)

Tam giác AHD vuông tại H có góc D = 30^o => tam giác AHD là nửa tam giác đều cạnh AD

=> 2AH=AD

<=> AH=AD/2=8/2=4(cm)

=> S_ABCD=CD.AH=7,5.4=30(cm²)

Xét ΔABD có 

\(cosBAD=\dfrac{AB^2+AD^2-BD^2}{2\cdot AB\cdot AD}\)

=>\(8^2+6^2-BD^2=2\cdot8\cdot6\cdot cos60=48\)

=>\(BD^2=100-48=52\)

=>\(BD=2\sqrt{13}\left(cm\right)\)

Xét ΔBAC có \(cosABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)

=>\(8^2+6^2-AC^2=2\cdot8\cdot6\cdot cos120=-48\)

=>\(AC^2=148\)

=>\(AC=2\sqrt{37}\left(cm\right)\)

2.8.6.cos60 tính như nào ra 48 đc vậy???

Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.

Suy ra:

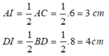
Xét tam giác AID có:  A I 2 + I D 2 = A D 2   ( 3 2 + 4 2 = 5 2 = 25 )

Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD

Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi.

Suy ra: AB = BC = CD = DA = 5cm

Chọn đáp án B