Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Biết OB = 3cm; OA = 5cm. Câu nào sau đây sai?
A \(\widehat{BOA}\) = \(\widehat{CAO}\)
B OB = OC
C \(\widehat{BAO}\)=\(\widehat{CAO}\)
D AB = AC = 4cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

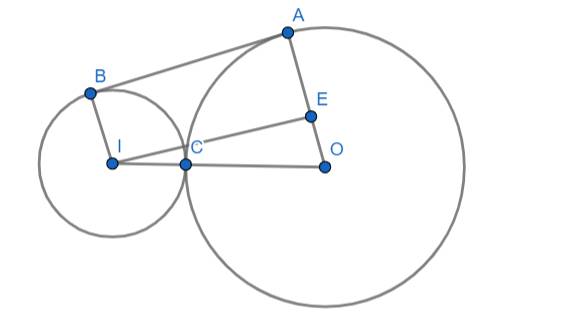
Do AB là tiếp tuyến chung của (O) và (I) nên:
\(\left\{{}\begin{matrix}\widehat{IBA}=90^o\\\widehat{OAB}=90^o\end{matrix}\right.\) (tiếp tuyến vuông góc với bán kính)
\(\Rightarrow\left\{{}\begin{matrix}IB\perp AB\\OA\perp AB\end{matrix}\right.\)
\(\Rightarrow IB//OA\) (cùng vuông góc với AB)
\(\Rightarrow ABOI\) là hình thang
Ta kẻ IE vuông góc với OA tại E
⇒ IEAB là hình chữ nhật
⇒ \(IB=AE=2\left(cm\right)\) (cặp cạnh đối của hình chữ nhật)
\(\Rightarrow OE=OA-AE=8-2=6\left(cm\right)\)
Mà: \(OI=OC+IC=2+8=10\left(cm\right)\)
Xét ΔIEO vuông tại E áp dụng định lý Py-ta-go ta có:
\(IO^2=OE^2+IE^2\)
\(\Leftrightarrow10^2=6^2+IE^2\)
\(\Leftrightarrow IE=\sqrt{100-36}=\sqrt{64}\)
\(\Leftrightarrow IE=8\left(cm\right)\)
Mà: \(AB=IE=8\left(cm\right)\) (ABIE là hình chữ nhật)
Diện tích của tứ giác ABOI có AB là đường cao là:
\(S_{ABOI}=\dfrac{\left(IB+OA\right)\cdot AB}{2}=\dfrac{\left(2+8\right)\cdot8}{2}=40\left(cm^2\right)\)

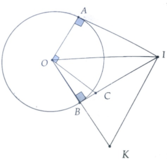
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H
b, IA=12cm
Chứng minh ΔKOI cân tại K
Đặt KO = KI = x (x>0)
Có I K 2 = I B 2 + B K 2
Hay x 2 = 12 2 + x - 9 2
=> x = 12,5 => IK = 12,5cm

OB=căn18
b> Xét 2 tam giác bằng nhau đó là tam giác OAB=BCO là ra 2 góc cần xét
ta có tam giác AOC cân và OH là đường cao nên cũng là đường phân giác =>OAH=HOC
xét 2 tam giác OAB và tam giÁC BCO có OA=OB (bán kính )AOH=HOC(cmt) OB CHUNG => AOB=BCO(C-G-C)=>GÓC OAB=BCO hay OC vuông BC=>...............
AC=3
Chon A