Xét tứ giác MIOK có

\(\widehat{MIO}+\widehat{MKO}=90^0+90^0=180^0\)

=>MIOK là tứ giác nội tiếp

=>M,I,O,K cùng thuộc một đường tròn

lấy A là trung điểm của OM,xét tam giác OMI có:
A là trung điểm của OM
O,M,I thuộc 1 đường tròn. (1)
Xét tam giác OMK có A là trung điểm của OM
O,M,K thuộc 1 đường tròn (2)
từ (1) và (2) suy ra 4 điểm M,I,O,K cùng thuộc 1 đường tròn
 

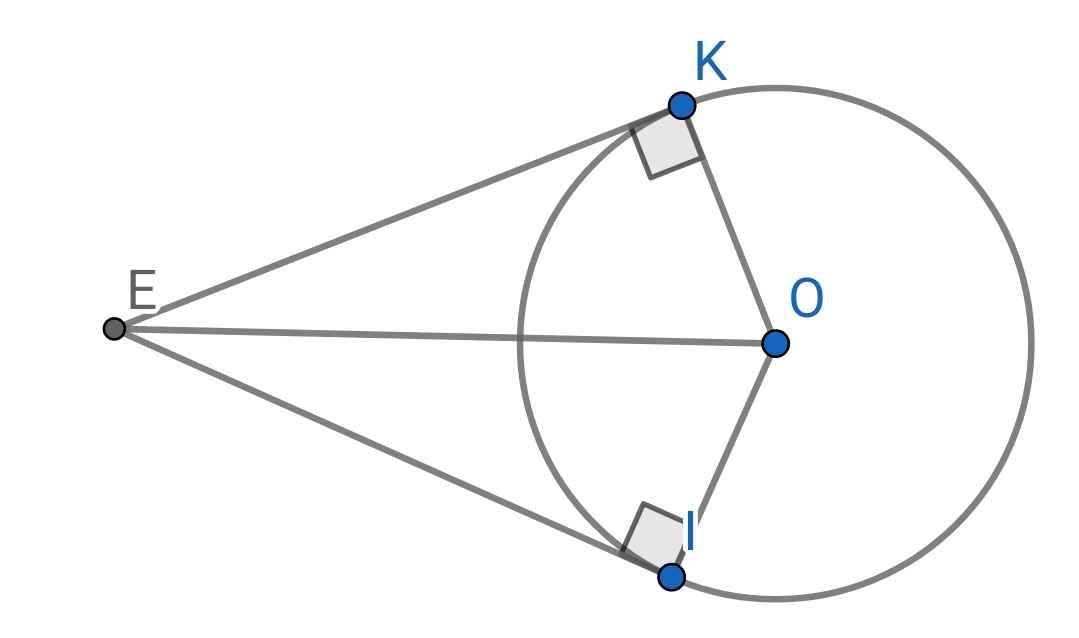  Do EI là tiếp tuyến của (O) tại I

⇒ EI OI

⇒ ∆OEI vuông tại I

⇒ O, E, I cùng thuộc đường tròn đường kính OE  (1)

Do EK là tiếp tuyến của (O) tại K

⇒ EK OK

⇒ ∆OEK vuông tại K

⇒ O, E, K cùng thuộc đường tròn đường kính OE  (2)

Từ (1) và (2) suy ra E, I, O, K cùng thuộc đường tròn đường kính OE

Lời giải:

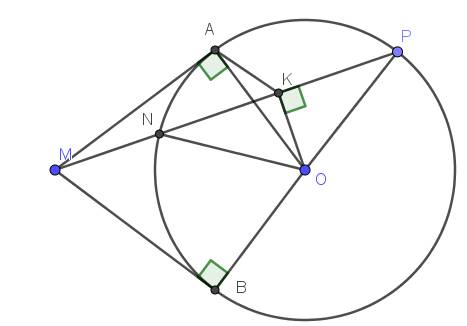
Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$

$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$

Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.

$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)

Mặt khác:

Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.

$\Rightarrow \widehat{MKO}=90^0$

Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.

$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)

Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.

Lời giải:

Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$

$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$

Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.

$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)

Mặt khác:

Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.

$\Rightarrow \widehat{MKO}=90^0$

Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.

$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)

Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.

Hình vẽ:

a: Xét tứ giác KBOD có

\(\widehat{OBK}+\widehat{ODK}=180^0\)

=>KBOD là tứ giác nội tiếp

b: Xét (O) có

KB,KD là tiếp tuyến

=>KB=KD

mà OB=OD

nên OK là trung trực của BD

=>OK cắt BD tại trung điểm của BD

=>O,I,K thẳng hàng và OK\(\perp\)BD tại I

Xét ΔKBA và ΔKCB có

\(\widehat{KBA}=\widehat{KCB}\)

\(\widehat{BKA}\) chung

Do đó: ΔKBA đồng dạng với ΔKCB

=>KB/KC=KA/KB

=>\(KB^2=KA\cdot KC\)(1)

Xét ΔKBO vuông tại B có BI là đường cao

nên \(KI\cdot KO=KB^2\left(2\right)\)

Từ (1) và (2) suy ra \(KA\cdot KC=KI\cdot KO\)

cho xin cái hình