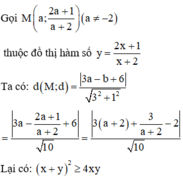
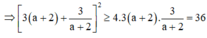
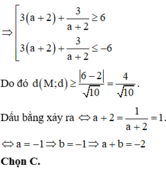
a) Với ∆ABC ⊥ tại A và M là trung điểm BC, ta có:

- Theo định lý Pythagoras, ta có: AB^2 + AC^2 = BC^2

- Thay giá trị vào, ta có: 6^2 + 8^2 = BC^2

- Tính toán, ta có: 36 + 64 = BC^2

- Tổng cộng, BC^2 = 100

- Vì BC là độ dài, nên BC = √100 = 10cm

- Vì M là trung điểm BC, nên AM = MC = 10/2 = 5cm

b) Để chứng minh ABEC là hình chữ nhật, ta cần chứng minh AB // EC và AB = EC.

- Vì M là trung điểm BC, nên AM = MC.

- Vì ∆ABC ⊥ tại A, nên góc BAC = 90 độ.

- Vì M là trung điểm BC, nên BM = MC.

- Vì BM = MC và góc BAC = 90 độ, nên ∆BAM ≅ ∆CAM theo góc-góc-góc.

- Từ đó, ta có AB = AC và góc BAM = góc CAM.

- Vì AB = AC và góc BAM = góc CAM, nên ∆ABM ≅ ∆ACM theo cạnh-góc-cạnh.

- Từ đó, ta có góc AMB = góc AMC và BM = MC.

- Vì góc AMB = góc AMC và BM = MC, nên ∆BME ≅ ∆CME theo góc-góc-góc.

- Từ đó, ta có góc BME = góc CME và BM = MC.

- Vì góc BME = góc CME và BM = MC, nên BM // EC.

- Vì BM // EC và AB = AC, nên AB // EC và AB = EC.

- Từ đó, ta có ABEC là hình chữ nhật.

c) Để chứng minh AH = IK và NO = 1/2 IK, ta cần chứng minh ∆AHN ≅ ∆IKO.

- Vì AH ⊥ BC và IK ⊥ AB, nên góc HAN = góc KIO = 90 độ.

- Vì AH ⊥ BC và HN ⊥ AN, nên góc HAN = góc HNA.

- Vì IK ⊥ AB và KO ⊥ AO, nên góc KIO = góc KOI.

- Vì góc HAN = góc HNA và góc KIO = góc KOI, nên ∆AHN ≅ ∆IKO theo góc-góc-góc.

- Từ đó, ta có AH = IK và NO = 1/2 IK.

d) Vì ∆AHN ≅ ∆IKO, nên góc INK = góc HNO.

- Vì NO = 1/2 IK, nên góc HNO = góc INK.

- Từ đó, ta có góc INK = góc HNO.

bạn có thể chỉ mình cách vẽ hình câu c được ko

a: Xét tứ giác AHBE có

M là trung điểm của AB

M là trung điểm của HE

Do đó: AHBE là hình bình hành

mà \(\widehat{AHB}=90^0\)

nên AHBE là hình chữ nhật

b: Xét tứ giác ABFC có

H là trung điểm của AF

H là trung điểm của BC

Do đó:ABFC là hình bình hành

mà AB=AC

nên ABFC là hình thoi

a) Ta có: E đối xứng với H qua M (gt)

=> M là trung điểm của HE

Xét tứ giác AHBE có:

MA = MB (M là trung điểm của AB)

ME = MH (M là trung điểm của HE)

\(\widehat{AHB}=90^o\)(Vì AH là đường cao vuông góc với BC)

=> AHBE là hcn (đpcm)

b, Vì ABC là tam giác cân

=> AB = AC (1)

Vì F đối xứng với A qua H

=> FB = AB ; FC = AC (2)

Từ (1) và (2) => AB = AC = FC = FB

Xét tứ giác ABFC có: AB = AC = FC = FB (cm trên)

=> ABFC là hình thoi (đpcm) 

a: \(BC=\sqrt{6^2+12^2}=6\sqrt{5}\left(cm\right)\)

=>\(IM=\dfrac{AB}{2}=3cm\)

b: Xét tứ giác ABCD có

ID//AB

IA//DB

góc IAB=90 độ

IA=AB

Do đó: ABCD là hình vuông

Giúp với :<