Cho ba số thực dương \(a;b;c\) thỏa mãn \(a^2+b^2+c^2=3\) . Chứng minh rằng :\(\dfrac{a}{\sqrt{a^2+b+c}}+\dfrac{b}{\sqrt{b^2+a+c}}+\dfrac{c}{\sqrt{c^2+b+a}}\le\sqrt{3}\) P/s: Em xin phép nhờ sự giúp đỡ và gợi ý của quý thầy cô giáo và các bạn yêu toán...
Đọc tiếp
Cho ba số thực dương \(a;b;c\) thỏa mãn \(a^2+b^2+c^2=3\) . Chứng minh rằng :
\(\dfrac{a}{\sqrt{a^2+b+c}}+\dfrac{b}{\sqrt{b^2+a+c}}+\dfrac{c}{\sqrt{c^2+b+a}}\le\sqrt{3}\)
P/s: Em xin phép nhờ sự giúp đỡ và gợi ý của quý thầy cô giáo và các bạn yêu toán ạ!
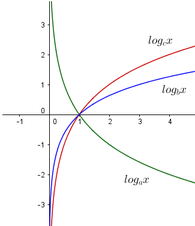
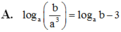
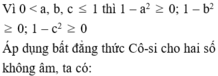
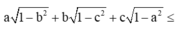
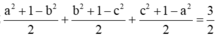
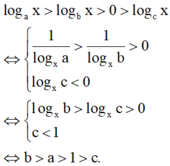
Ta có:
\(\left(a^2+b+c\right)\left(1+b+c\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow\dfrac{a}{\sqrt{a^2+b+c}}\le\dfrac{a\sqrt{1+b+c}}{a+b+c}\)
Tương tự: \(\dfrac{b}{\sqrt{b^2+a+c}}\le\dfrac{b\sqrt{1+c+a}}{a+b+c}\) ; \(\dfrac{c}{\sqrt{c^2+b+a}}\le\dfrac{c\sqrt{1+a+b}}{a+b+c}\)
Cộng vế:
\(P\le\dfrac{a\sqrt{1+b+c}+b\sqrt{1+c+a}+c\sqrt{1+a+b}}{a+b+c}\)
Lại có:
\(a\sqrt{1+b+c}+b\sqrt{1+c+a}+c\sqrt{1+a+b}\)
\(=\sqrt{a}.\sqrt{a+ab+ac}+\sqrt{b}.\sqrt{b+bc+ab}+\sqrt{c}.\sqrt{c+ac+bc}\)
\(\le\sqrt{\left(a+b+c\right)\left(a+b+c+2ab+2bc+2ca\right)}\)
\(\Rightarrow P\le\dfrac{\sqrt{\left(a+b+c\right)\left(a+b+c+2ab+bc+ca\right)}}{a+b+c}=\sqrt{\dfrac{a+b+c+2ab+2bc+2ca}{a+b+c}}\)
Do đó ta chỉ cần chứng minh:
\(\dfrac{a+b+c+2ab+2bc+2ca}{a+b+c}\le3\Leftrightarrow a+b+c\ge ab+bc+ca\)
Thật vậy:
\(\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)=\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)\ge\left(ab+bc+ca\right)^2\)
\(\Rightarrow a+b+c\ge ab+bc+ca\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)