Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song với AC, AB; chúng
cắt AB, AC tại E, F. Chứng minh tỉ lệ thức:AE/AB+AF/AC=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 2 2018
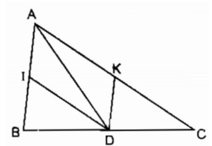
Ta có: DK // AB (gt)
hay DK // AI
DI // AC (gt)
hay DI // AK
Vậy tứ giác AIDK là hình bình hành
CM
21 tháng 4 2019
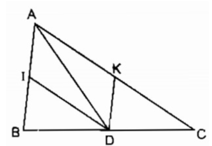
Để hình bình hành AIDK là hình thoi.
⇒ AD là đường phân giác của ∠ (IAK)
hay AD là đường phân giác của ∠ (BAC)
Ngược lại nếu AD là tia phân giác của ∠ (BAC)
Ta có tứ giác AIDK là hình bình hành có đường chéo AD là phân giác của góc A nên tứ giác AIDK là hình thoi
Vậy hình bình hành AIDK là hình thoi khi và chỉ khi D là giao điểm tia phân giác của góc A và cạnh BC.
3 tháng 3 2023
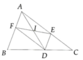
a: ΔCEF đồng dạng với ΔCAB theo tỉ số k=CE/CA
ΔADE đồng dạng với ΔABC
=>k'=AD/AB=2/5
b: \(\dfrac{C_{ADE}}{C_{ABC}}=\dfrac{AD}{AB}=\dfrac{2}{5}\)
=>\(C_{ADE}=\dfrac{2}{5}\cdot\left(5+7+9\right)=\dfrac{2}{5}\cdot21=\dfrac{42}{5}\left(cm\right)\)
ΔCEF đồng dạng với ΔCAB
=>\(\dfrac{C_{CEF}}{C_{CAB}}=\dfrac{CE}{CA}=\dfrac{3}{5}\)
=>\(C_{CEF}=\dfrac{3}{5}\cdot\left(5+7+9\right)=\dfrac{3}{5}\cdot21=\dfrac{63}{5}\left(cm\right)\)
CM
19 tháng 4 2017
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
⚡
20 tháng 12 2015
434
AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!
AE/AB=DC/BC
AF/AC=BD/BC
=>AE/AB+AF/AC=(DC+BD)/BC=1
mấy anh chị nhanh quá, em ms vừa đọc câu hỏi, hic