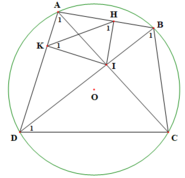
a) Tứ giác AHIK có:

A H I ^ = 90 0   ( I H ⊥ A B ) A K I ^ = 90 0   ( I K ⊥ A D ) ⇒ A H I ^ + A K I ^ = 180 0

=> Tứ giác AHIK nội tiếp.

b) ∆ IAD và  ∆ IBC có:

A ^ 1 = B ^ 1  (2 góc nội tiếp cùng chắn cung DC của (O))

A I D ^ = B I C ^  (2 góc đối đỉnh)

=> ∆ IAD ~   ∆ IBC (g.g)

⇒ I A I B = I D I C ⇒ I A . I C = I B . I D

c, Xét đường tròn ngoại tiếp tứ giác AHIK có K ^ 1 = D ^ 1

A ^ 1 = H ^ 1  (2 góc nội tiếp cùng chắn cung IK)

mà  A ^ 1 = B ^ 1 ⇒ H ^ 1 = B ^ 1

Chứng minh tương tự, ta được K ^ 1 = D ^ 1

∆ HIK và  ∆ BCD có:  H ^ 1 = B ^ 1  ;  K ^ 1 = D ^ 1

=>   ∆ HIK  ~   ∆ BCD (g.g)

d) Gọi S₁ là diện tích của  ∆ BCD.

Vì  ∆ HIK  ~   ∆ BCD nên:

S ' S 1 = H K 2 B D 2 = H K 2 ( I B + I D ) 2 ≤ H K 2 4 I B . I D = H K 2 4 I A . I C                                 (1)

Vẽ  A E ⊥ B D  ,  C F ⊥ B D ⇒ A E / / C F ⇒ C F A E = I C I A  

∆ ABD và  ∆ BCD có chung cạnh đáy BD nên:

S 1 S = C F A E ⇒ S 1 S = I C I A                                                                     (2)

Từ (1) và (2) suy ra

S ' S 1 ⋅ S 1 S ≤ H K 2 4 I A . I C ⋅ I C I A ⇔ S ' S ≤ H K 2 4 I A 2  (đpcm)