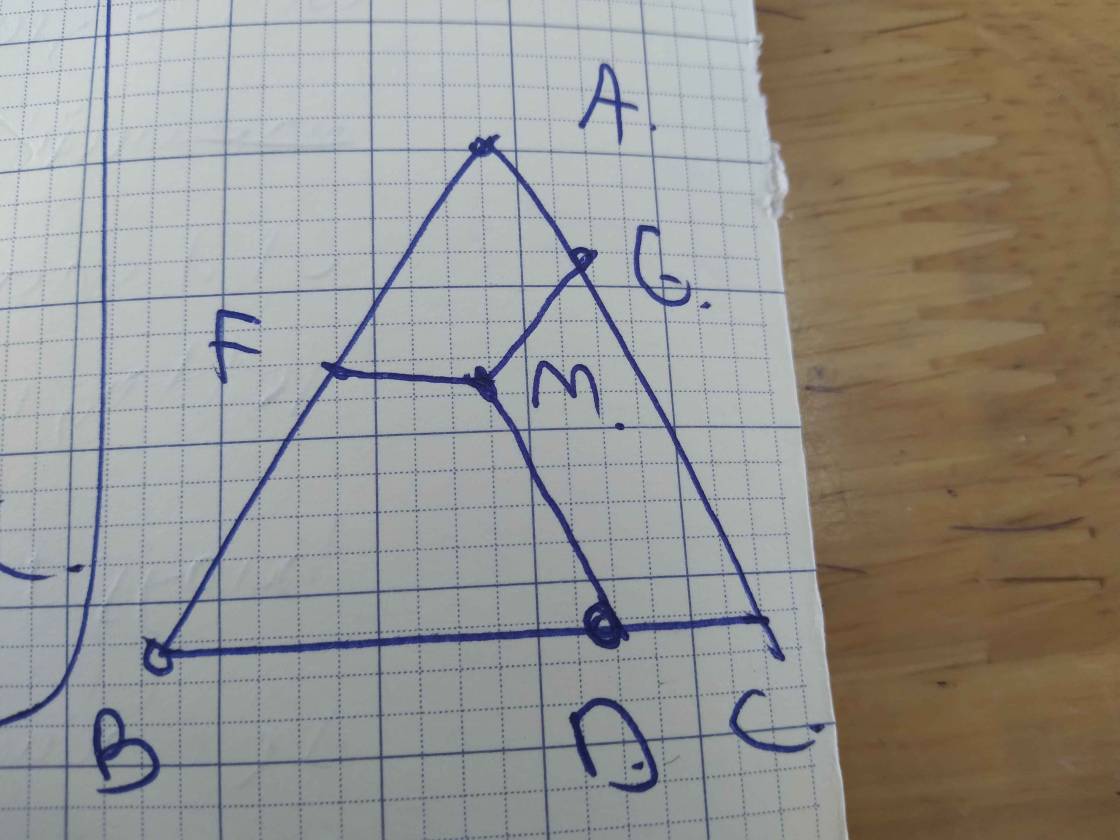
Cho tam giác dều ABC .điểm M nằm giữa B và C.đường thẳng kẻ qua M và song song với AC cắt AB ở P,đường thẳng kẻ qua M và song song AB cắt AC ở N
a/ CM tam giác BPM là tam giác đều
b/gọi I là giao điểm của AM và PN,gọi O là trọng tâm của tam giác ABC.CM rằng tam giác OAN bằng tam giác OBP
c/gọi H là một điểm trên đường thẳng BC sao cho HP=HN .CM rằng ba điểm H,I,O thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 4 2018
a) MP // AC => ^MPB=^CAB; ^PMB=^ACB. Mà ^CAB=^ACB=600
=> ^MPB=^PMB=600 => Tam giác BPM là tam giác đều (đpcm).
b) Tam giác BPM là tam giác đều (cmt) => PM=BP
Ta có: PM//AN; M//AP => PM=AN (Tính chất đoạn chắn)
=> BP=AN.
Tam giác ABC đều và O là trọng tâm nên ta có: ^OBA=^OAC=300 hay ^OBP=^OAN và OB=OA
Xét tam giác OAN và tam giác OBP: BP=AN; OA=OB; ^OAN=^OBP
=> Tam giác OAN= Tam giác OBP (đpcm)
c) Tam giác AIP=Tam giác MIN (g.c.g) => IP=IN hay I là trung điểm của NP
Tam giác OAN=Tam giác OBP (cmt) => ON=OP => O nằm trên trung trực của NP (1)
HP=HN => H nằm trên trung trực của NP (2)
Từ (1) và (2) kết hợp với I là trung điểm của NP => H;I;O thẳng hàng (đpcm).
15 tháng 6 2018
a, Xét ∆ ABC đều
➡️Góc A = góc B = góc C = 60°
Vì MN // AB (gt)
➡️Góc ABC = góc NMC = 60°
Xét ∆ MNC có 2 góc bằng 60°
➡️∆ MNC đều
C/m tương tự ta sẽ có ∆ BMP đều
b, ✳️ Ta có: MN // AB
MP // AC
➡️AN = MP (t/c cặp đoạn chắn)
mà MP = BP (∆ BMP đều)
➡️AN = BP
T/c cặp đoạn chắn: hai đoạn thẳng song song bị chắn bởi hai đoạn thẳng song song thì bằng nhau.
✳️ Vì ∆ ABC đều
➡️O là trọng tâm đồng thời là tâm đg tròn ngoại tiếp
➡️OA = OB
O cx đồng thời là tâm đg tròn nội tiếp
➡️AO là tia phân giác của góc BAC
➡️Góc BAO = góc OAN (1)
✳️ Xét ∆ ABO có OA = OB (cmt)
➡️∆ ABO cân tại O
➡️Góc ABO = góc BAO (2)
Từ (1) và (2) ➡️góc ABO = góc OAN
✳️ Xét ∆ AON và ∆ BOP có:
AN = BP (cmt)
Góc OAN = góc ABO (cmt)
OA = OB (cmt)
➡️∆ AON = ∆ BOP (c.g.c)
c, Vì ∆ AON = ∆ BOP (cmt)
➡️ON = OP (2 cạnh t/ư)
➡️OI là đg trung trực của PN (đpcm)
Mk trình bày đầy đủ rồi đó bn chỉ cần viết vào vở thôi mk nha hok tốt~
CL
15 tháng 11 2023
a, Xét tứ giác MNPB có:
MN//PB (Vì MN//BC và P ϵ BC)
MB//NP (Vì AB//NP và M ϵ AB)
=> Tứ giác MNPB là hbh
b, Ta có:
M là trung điểm AB
MN//BC
=> MN là đường trung bình của tam giác ABC
=> N là trung điểm AC, MN=BC/2 và MN//BC
Xét 2 tam giác AMN và NPC có
AM=NP (Vì AM=BM, BM=NP)
AN=NC
MN=PC ( Vì MN=BC/2, MN=BP)
=> Tam giác AMN = Tam giác NPC (c.c.c)