1: \(S_{ABCD}=\dfrac{1}{2}\cdot AH\cdot\left(AB+CD\right)\)

=>\(\left(AB+3AB\right)\cdot\dfrac{1}{2}\cdot3=30\)

=>4AB=20

=>AB=5(m)

CD=3*AB=15(m)

2:

Xét ΔEAB có AB//CD

nên \(\dfrac{EA}{ED}=\dfrac{AB}{CD}\)

=>\(\dfrac{EA}{ED}=\dfrac{1}{3}\)

Xét ΔEAB và ΔEDC có

\(\widehat{E}\) chung

\(\dfrac{EA}{ED}=\dfrac{EB}{EC}\)

Do đó: ΔEAB đồng dạng với ΔEDC

=>\(\dfrac{S_{EAB}}{S_{EDC}}=\left(\dfrac{AB}{DC}\right)^2=\dfrac{1}{9}\)

=>\(\dfrac{S_{EAB}}{S_{ABCD}}=\dfrac{1}{8}\)

=>\(S_{EAB}=\dfrac{30}{8}=3,75\left(m^2\right)\)

Giải: Diện tích hình thang ABCD là: (60 + 40) x 40 : 2 = 2000 ()

Nối G với A và nối G với D ta có:

Diện tích tam giác GBA là: 40 x 30 : 2 = 600 ()

Diện tích tam giác GDC là: 60 x 10 : 2 = 300 ()

Diện tích tam giác AGD là: 2000 - (600 + 300) = 1100 ()

Độ dài cạnh EG là: 1100 x 2 : 40 = 55 (m)

Diện tích hình thang ABGE là: (55 + 40) x 30 : 2 = 1425 ()

Diện tích hình thang EGCD là: (60 + 55) x 10 : 2 = 575 ()

Đáp số: S. ABGE: 1425 (); S. EGCD: 575 ()

Giải: Diện tích hình thang ABCD là: (60 + 40) x 40 : 2 = 2000 ()

Nối G với A và nối G với D ta có:

Diện tích tam giác GBA là: 40 x 30 : 2 = 600 ()

Diện tích tam giác GDC là: 60 x 10 : 2 = 300 ()

Diện tích tam giác AGD là: 2000 - (600 + 300) = 1100 ()

Độ dài cạnh EG là: 1100 x 2 : 40 = 55 (m)

Diện tích hình thang ABGE là: (55 + 40) x 30 : 2 = 1425 ()

Diện tích hình thang EGCD là: (60 + 55) x 10 : 2 = 575 ()

Đáp số: S. ABGE: 1425 (); S. EGCD: 575 ()

Gọi giao của BC và AD là M

Xét ΔMDC có AB//DC
nên MA/(MA+40)=40/60=2/3

=>3MA=2MA+80

=>MA=80cm

Xét ΔMEG có AB//EG

nên AB/EG=MA/ME

=>40/EG=80/110=8/11

=>EG=40:8/11=55(cm)

\(S_{ABGE}=\dfrac{1}{2}\cdot30\cdot\left(40+55\right)=95\cdot15=1425\left(cm^2\right)\)

Kéo dài AB về phía B một đoạn BE=DC. Nối DE cắt BC tại M.

Do CD // BE nên ta có tam giác MDC = tam giác MEB (trường hợp g.c.g). Suy ra dt(ABCD)=dt(ABMD) + dt(MDC) = dt(ABMD) + dt(MEB) = dt(DAE) = 1/2 .AE . h =1/2 (AB + BE).h = \(\dfrac{AB+CD}{2}.h\)

b) Theo câu a) thì diện tích hình thang ABCD bằng diện tích tam giác DAE nên ta nối D với trung điểm N của AE thì DN sẽ chia tam giác DAE thành 2 phần bằng nhau. Khi đó diện tích tam giác DAN bằng nửa diện tích hình thang ABCD.

Diện tích hình thang ABCD là:

        (60 + 40) x 40 : 2 = 2000 (m2)

Khi nối G với A và nối G với D ta có:

Diện tích tam giác GBA là:

        40 x 30 : 2 = 600 (m2)

Diện tích tam giác GDC là:

        60 x 10 : 2 = 300 (m2)

Diện tích tam giác AGD là:

        2000 - (600 + 300) = 1100 (m2)

Độ dài cạnh EG là:

        1100 x 2 : 40 = 55 (m)

Diện tích hình thang ABGE là:

        (55 + 40) x 30 : 2 = 1425 (m2)

Diện tích hình thang EGCD là:

        (60 + 55) x 10 : 2 = 575 m2

Đáp số: ABGE: 1425 m2

              EGCD: 575 m2

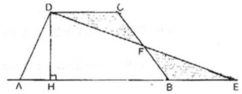
Gọi F là trung điểm của cạnh bên BC. Cắt hình thang theo đường DF đưa ghép về như hình vẽ bên, điểm C trung với điểm B, D trùng với E.

Vì AB // CD ⇒ ∠ (ABC) = 180 0 ⇒ A, B, E thẳng hàng

∠ (ABF) +  ∠ (DFC) =  180 0

⇒ D, F, E thẳng hàng

△ DFC = △ EFB (g.c.g)

S D F C = S E F B

Suy ra: S A B C D = S A D E

△ DFC =  △ EFB⇒ DC = BE

AE = AB + BE = AB + DC

S A D E  = 1/2 DH. AE = 1/2 DH. (AB + CD)

Vậy : S A B C D = 1/2 DH. (AB + CD)

Độ dài đáy lớn là:

\(12\cdot2=24\left(cm\right)\)

Tổng độ dài 2 đáy là:

\(12+24=36\left(cm\right)\)

Một nửa diện tích hình thang là:

\(180:2=90\left(cm\right)\)

Đường cao hình thang có độ dài là:

\(90:36=2,5\left(cm\right)\)

Đáp số: \(2,5cm\)

giải: 

đáy lớn là: 12x2=24

chiều cao là: 180x2:(12+24)= 10(cm)