cách tìm GTNN và GTLN và tìm số nguyên của một biểu thức ta làm như thế nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì | x -3 | > hoặc = 0
Suy ra : |x-3|+50 >hoặc =50
Vì A nhỏ nhất suy ra | x-3 | +50 =50
Suy ra x-3 =0
Suy ra x=3
Vậy GTNN của A = 50 khi x=3

Vd : \(x^2+6x+10\)
Ta có : 10 không căn được
Mà : \(x^2+2.x.3+3^2\)
Nhưng 32 chỉ là 9 nên ta cộng thêm 1 ở vế sau
\(\left(x^2+2.x.3+3^2\right)+1\)
\(\left(x+3\right)^2+1\)
Dư 1 ở ngoài :
Vì \(\left(x+3\right)^2\ge0\)
=> \(\left(x+3\right)^2+1\ge1\)
=> GTNN là 1
Khi ( x + 3 ) = 0
x = -3
Khi
Giải
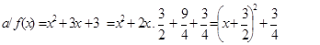
Ta có 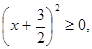 nên
nên 
Vậy: f(x) đạt GTNN bằng  khi
khi 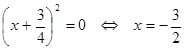
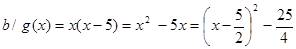
Ta có  nên
nên 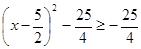
Vậy: g(x) đạt GTNN bằng  khi
khi 

Bạn làm nhiều bài tập rồi quen dần với mấy dạng này ,chứ chỉ ra cách nào thì khó lắm
Thường thì biến đổi về. Dạng bình phương (cũng có những cách khác nhé)
Ví du:tim giá trị nhỏ nhất của:x^2+2x+2=(x+1)^2+1 lớn hơn hoặc bằng 1 với mọi x thuộc R

Đây là một câu hỏi quá rộng nên rất khó để trả lời.
Tìm được max hay min thì có nhiều phương pháp, đã được đề cập trong nhiều đầu sách/ tài liệu.
Thông thường phân thức người ta sẽ nói rõ là tìm max hay min rồi.
Đối với phân thức mà người ta nói tìm max hoặc min (không nói rõ), nếu ta thấy nó có những điều kiện để xảy ra dấu $\geq$ thì nó có min và ngược lại, nó có những điều kiện để tạo ra dấu $\leq$ thì nó có max. Còn điều kiện là gì thì tùy bài quyết định.

\(#\)GTNN đưa về dạng \(A^2+m\) với \(m\) là hằng số khi đó ta được \(A^2\)\(+m\) ≥\(m\) sau đó tìm dấu "=" xảy ra khi nào ( Dấu bằng xảy ra khi A\(^2\)\(=0\)) sau đó kết luận .
VD : Tìm GTNN của \(A=\)\(x^2+2x+3\)
A \(=\left(x^2+2x+1\right)+2\)\(=\left(x+1\right)^2+2\) ≥ \(2\)
Dấu "=" xảy ra khi \(\left(x+1\right)^2=0=>x=-1\)
Vậy \(A_{min}=2< =>x=-1\)
\(#\)GTLN đưa về dạng \(k-B^2\) với \(k\) là hằng số khi đó ta tìm được \(k-B^2\)≤ \(k\) sau đó tìm dấu "=" xảy ra khi nào ( Dấu bằng xảy ra khi \(B^2=0\)) sau đó kết luận.
VD Tìm GTLN của \(B=10+4x-x^2\)
B\(=-x^2+4x-4+14\)\(=14-\left(x^2-4x+4\right)\)\(=14-\left(x-2\right)^2\) ≤ 14
Dấu "=" xảy ra khi \(\left(x-2\right)^2=0=>x=2\)
Vậy \(B_{max}=14< =>x=2\)