a, xét ΔABDvàΔHBDΔABDvàΔHBD có

AD chung

ABDˆ=HBDˆABD^=HBD^ ( AD là tia phân giác của ABCˆABC^ )

Aˆ=Hˆ=900A^=H^=900

=> ΔΔ ABD = ΔΔHBD ( ch - gn )

b, xét ΔKADvàΔCHDΔKADvàΔCHD có

AK = HC ( gt)

AD = DH ( câu a )

Aˆ=Hˆ=900A^=H^=900

=> ΔAKD=ΔHDCΔAKD=ΔHDC

=> ADKˆ=HDCˆADK^=HDC^ mà 2 góc này ở vị trí đối đỉnh

=> đpcm

a, Xét \(\Delta\)ABD và \(\Delta\)HBD có

AD_chung

^ABD = ^HBD  ( AD là tia p/g của ^ABC )

^A = ^H ( = 90⁰ )

=> \(\Delta\)ABD = \(\Delta\)HBD (ch-gn)

b, Xét \(\Delta\)KAD và \(\Delta\)CHD có

AK = HC (gt)

AD = DH (câu a)

^A = ^H ( = 90⁰ )

=> \(\Delta\)AKD =\(\Delta\)HDC

=> ^ADK = ^HDC (đđ) 

Vậy  3 điểm K,D,H thẳng hàng

Sửa đề: DH vuông góc với BC

a) Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))

Do đó: ΔABD=ΔHBD(cạnh huyền-góc nhọn)

b) Ta có: ΔABD=ΔHBD(cmt)

nên DA=DH(hai cạnh tương ứng)

Xét ΔADK vuông tại A và ΔHDC vuông tại H có 

DA=DH(cmt)

AK=HC(gt)

Do đó: ΔADK=ΔHDC(hai cạnh góc vuông)

Suy ra: DK=DC(hai cạnh tương ứng)

Ta có: BA+AK=BK(A nằm giữa B và K)

BH+HC=BC(H nằm giữa B và C)

mà BA=BH(ΔBAD=ΔBHD)

và AK=HC(gt)

nên BK=BC

Ta có: BK=BC(cmt)

nên B nằm trên đường trung trực của CK(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: DK=DC(cmt)

nên D nằm trên đường trung trực của CK(Tính chất đường trung trực của một đoạn thẳng)(2)

TỪ (1) và (2) suy ra BD là đường trung trực của CK

hay BD⊥CK

Xét ΔBKC có 

BD là đường cao ứng với cạnh KC(cmt)

CA là đường cao ứng với cạnh BK(gt)

CA cắt BD tại D(gt)

Do đó: D là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)

Suy ra: KD là đường cao ứng với cạnh BC

mà DH là đường cao ứng với cạnh BC(gt)

và KD, DH có điểm chung là D

nên K,D,H thẳng hàng(đpcm)

ae giúp mk với mai nộp rùi, tui chỉ mắc câu b) nữa thôi

Tam giác ABD=Tam giác HBD ??

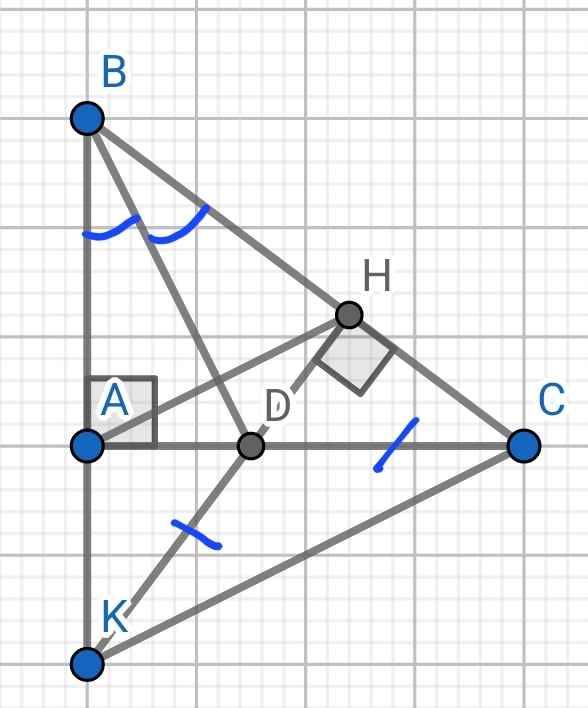
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:

BD chung

∠ABD = ∠HBD (BD là phân giác của ∠ABH)

⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)

b) Do ∆ABD = ∆HBD (cmt)

⇒ AB = BH (hai cạnh tương ứng)

⇒ B nằm trên đường trung trực của AH (1)

Do ∆ABD = ∆HBD (cmt)

⇒ AD = HD (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AH (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AH

c) Xét ∆ADK và ∆HDC có:

AD = HD (cmt)

∠ADK = ∠HDC (đối đỉnh)

DK = DC (gt)

⇒ ∆ADK = ∆HDC (c-g-c)

⇒ ∠DAK = ∠DHC (hai góc tương ứng)

⇒ ∠DAK = 90⁰

Mà ∠DAB = 90⁰

⇒ ∠DAK + ∠DAB = 180⁰

⇒ B, A, K thẳng hàng

a, Xét △ABD vuông tại A và △HBD vuông tại H

Có: ABD = HBD (gt)

       DB là cạnh chung

=> △ABD = △HBD (ch-gn)

b, Xét △ADK vuông tại A và △HDC vuông tại H

Có: AK = HC (gt)

       AD = HD (△ABD = △HBD)

=> △ADK = △HDC (cgv)

=> ADK = HDC (2 góc tương ứng)

Ta có: CDH + HDA = 180^o (2 góc kề bù)

=> ADK + HDA = 180^o

=> KDH = 180^o

=> 3 điểm K, D, H thẳng hàng.

a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔABD=ΔHBD

b: Ta có: ΔABD=ΔHBD

nên DA=DH

mà DH<DC

nên DA<DC

a: Xét ΔABD vuông tạiA  và ΔHBD vuông tại H có

BD chung

góc ABD=góc HBD

=>ΔBAD=ΔBHD

b: BA=BH

DA=DH

=>BD là trung trực của AH

c: Xét ΔDAK và ΔDHC có

DA=DH

góc ADK=góc HDC

DK=DC

=>ΔDAK=ΔDHC

=>góc DAK=góc DHC=90 độ

=>góc DAK+góc DAB=180 độ

=>B,A,K thẳng hàng

a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

góc ABD=góc HBD

=>ΔABD=ΔHBD

b: ΔBAD=ΔBHD

=>DA=DH

mà DH<DC

nên DA<DC