Bài 2: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.Tính độ dài đoạn BC.Bài 3: Bộ ba độ dài cho sau có thể là độ dài ba cạnh của một tam giác vuông không? Vì sao?a) 5cm, 12cm, 9cm b) 12 cm, 16 cm, 20 cmBài 4: Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE.a) Chứng minh: ΔABD = ΔACE. Bài 5: Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt AC tại D,...
Đọc tiếp
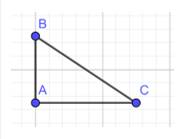
Bài 2: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.Tính độ dài đoạn BC.
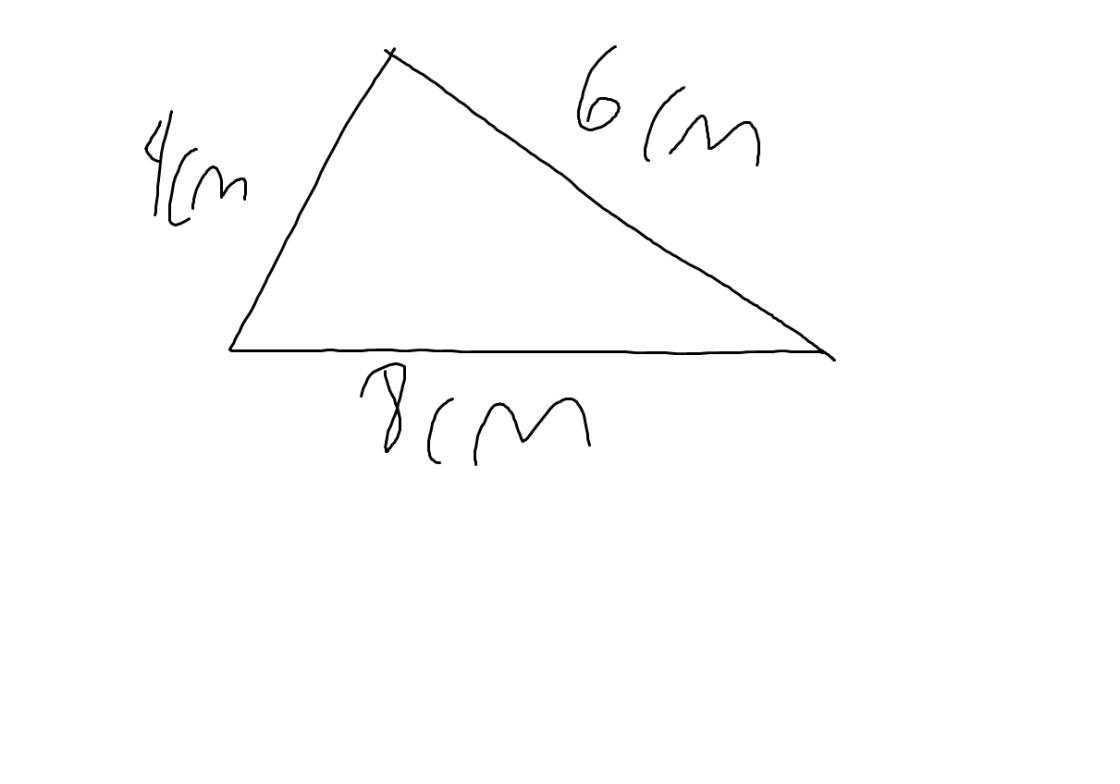
Bài 3: Bộ ba độ dài cho sau có thể là độ dài ba cạnh của một tam giác vuông không? Vì sao?
a) 5cm, 12cm, 9cm b) 12 cm, 16 cm, 20 cm
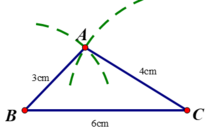
Bài 4: Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE.
a) Chứng minh: ΔABD = ΔACE.
Bài 5: Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt AC tại D, DN⊥BC tại N.
a) Chứng minh ∆DBA = ∆DBN. So sánh DA và DN.
b) Gọi M là giao điểm của hai đường thẳng ND và BA. Chứng minh AM = NC
c) Chứng minh ∆BMC cân.
Bài 10: Cho ΔABC vuông tại A, M là trung điểm của BC
a) Cho biết BC = 10cm, AC = 6cm. Tính độ dài đoạn thẳng AB.
b) Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh rằng ΔMAC = ΔMBD
c) Chứng minh AB // CD.
d) Chứng minh:
Bài 11: Cho tam giác ABC có BA < BC và
a)Trên BC lấy điểm M sao cho BM = BA. Chứng minh tam giác ABM đều.
b)Tia phân giác góc B cắt AC tại D. Chứng minh: ΔBAD = ΔBMD.
c)Tia MD cắt tia BA tại H, chứng minh ΔDHC cân.
Bài 12 : Cho tam giác ABC cân tại A, trên cạnh AB và AC lần lượt lấy hai điểm E và D sao cho AD = AE, BD cắt CE tại G. Chứng minh rằng:
a) BD = CE.
b) Tam giác GDE cân.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, G, M thẳng hàng.
d) Cho AB = 8 cm; MB = 5 cm. Tính độ dài AM?