1) Có \(\widehat{ABC}=\widehat{ADC}\)

\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ADC}\) \(\Leftrightarrow\widehat{EBC}=\widehat{CDF}\)

Xét \(\Delta BCE\) và \(\Delta DCF\) có:

\(\Leftrightarrow\widehat{EBC}=\widehat{CDF}\)

\(\widehat{E}=\widehat{F}=90^0\)

nên \(\Delta BCE\sim\Delta DCF\left(g.g\right)\) \(\Rightarrow\dfrac{CE}{CF}=\dfrac{CB}{CD}\) \(\Leftrightarrow CE.CD=CF.CB\)

Có \(\widehat{EAF}+\widehat{ECF}=360^0-\widehat{AEC}-\widehat{AFC}=360^0-90^0-90^0=180^0\)

mà \(\widehat{BAD}+\widehat{ABC}=180^0\) (hai góc so le trong do BC//AD)

\(\Rightarrow\widehat{ECF}=\widehat{ABC}\) (1)

mà \(CE.CD=CB.CF\) (cm trên)\(\Leftrightarrow CE.AB=CB.CF\) \(\Leftrightarrow\dfrac{CE}{CB}=\dfrac{CF}{AB}\) (2)

Từ (1);(2) \(\Rightarrow\Delta ABC\sim\Delta FCE\left(c.g.c\right)\)

2. Kẻ \(DK\perp AC\) tại K

Dễ chững minh được \(\Delta ADK\sim ACF\left(g.g\right)\)

\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AK}{AF}\Leftrightarrow AD.AF=AC.AK\) (*)

Dễ chứng minh được \(\Delta CDK\sim\Delta ACE\left(g.g\right)\)

\(\Rightarrow\dfrac{CK}{AE}=\dfrac{CD}{AC}\Leftrightarrow CK.AC=AE.CD\) mà DC=AB

\(\Rightarrow AB.AE=CK.AC\)  (3*)

Từ (*);(2*) cộng vế với vế \(\Rightarrow AB.AE+AD.AF=AC.CK+AC.AK=AC\left(CK+AK\right)\)

\(\Rightarrow AB.AE+AD.AF=AC^2\)

Vậy...

Dựng BG ⊥ AC.

Xét ΔBGA và ΔCEA, ta có:

∠ (BGA) =  ∠ (CEA) =  90 0

∠ A chung

⇒ △ BGA đồng dạng  △ CEA(g.g)

Suy ra: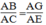 

AB.AE = AC.AG (1)

Xét  △ BGC và  △ CFA, ta có:

∠ (BGC) =  ∠ (CFA) = 90 0

∠ (BCG) =  ∠ (CAF) (so le trong vì AD //BC)

△ BGC đồng dạng △ CFA (g.g)

Suy ra: 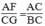 ⇒ BC.AF = AC.CG

Mà BC = AD (tính chất hình bình hành)

Suy ra: AD.AF = AC.CG (2)

Cộng từng vế đẳng thức (1) và (2) ta có:

AB.AE + AD.AF = AC.AG + AC.CG

AB.AE + AD.AF= AC(AG + CG)

Mà AG + CG = AC nên AB.AE + AD.AF =  A C 2

a, BE, DF cùng vuông góc vs AC nên BE//DF 
tam giác BEO = tam giác DFO ( cạnh huyền - góc nhọn) (O là gđ 2 đường chéo) 
=> BE = FD 
từ đó đc tg BEDF là hình bình hành 

b, tam giác BHC đồng dạng vs tam giác DKC (g.g) 
có góc H = góc k =90 độ 
và góc CBH = góc CDK ( vì 2 góc này kề bù vs 2 góc bằng nhau là góc CBA =góc ADC) 
=> BC/DC = HC/KC 
=>CB.CK = CH.CD 

c, tam giác ABE đồng dạng vs tam giác ACH (g.g) 
vì có góc E = góc H = 90 độ 
và góc A chung 
=> AB/AC = AE/AH 
=> AB. AH = AC.AE 

Tương tự ta đc tam giác ADF đồng dạng vs tam giác ACK 
=> AD/AC = AF/AK 
=> AD. AK = AC.AF 

Vậy AB.AH + AD.AK = AC.AE + AC.AF = AC. (AE +AF) = AC .( AE +CE) = AC^2 
tự chứng minh AF = CE theo tam giác vuông BEC = tam giác vuông DFA ( cạnh huyền - cạnh góc vuông) 

bạn ơi tại sao AB.AH+AD.AK=AC.AE+AC.AF