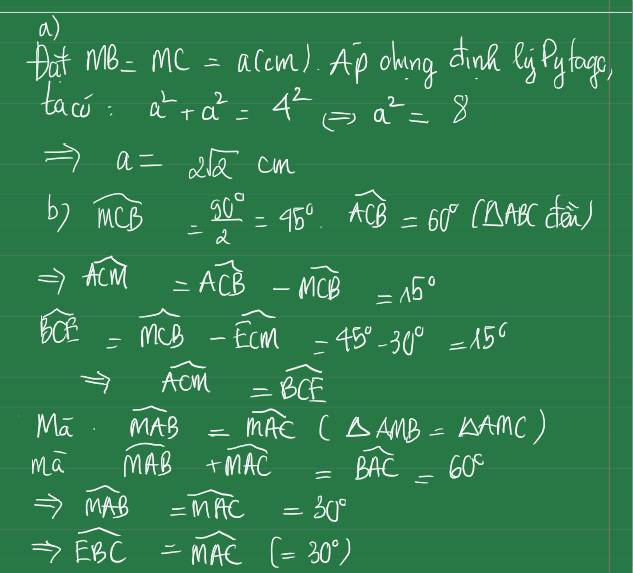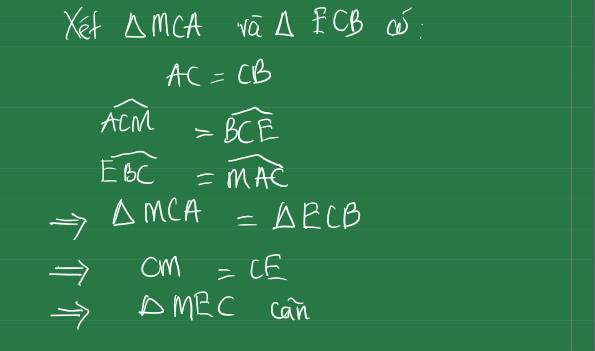mk ko bt lm câu b nha ~ xl

c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)

=> DM = AD = AM

Sau đó bạn chứng minh tam giác ADB = tam giác AMC (c.g.c) (cũng dễ thôi)

=> BD = MC (cặp cạnh tương ứng)

Ta có: DM = AM, BD = MC

=> DM : BM : BD = 3:4:5

=> tam giác BDM vuông tại M

=> góc AMB = 90o + 60o = 150o

a) Xét tam giác: AMB và AMC có:

AM chung

BM=CM ( gt)

AB=AC ( tam giác ABC đều)

=> Tam giác AMB =Tam giác AMC (1)

b) Xét tam giác MBC vuông cân tại M

=> \(\widehat{MCB}=\frac{90^o}{2}=45^o\)

Tam giác ABC đều 

=> \(\widehat{ACB}=60^o\)

=> \(\widehat{ACM}=\widehat{ACB}-\widehat{MCB}=60^o-45^o=15^o\)

\(\widehat{BCE}=\widehat{MCB}-\widehat{ECM}=45^o-30^o=15^o\)

=> \(\widehat{ACM}=\widehat{BCE}\)(2)

Từ (1) => \(\widehat{MAB}=\widehat{MAC}\) mà \(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}=60^o\)

=> \(\widehat{MAB}=\widehat{MAC}=60^o:2=30^o\)

=> \(\widehat{EBC}=\widehat{MAC}\left(=30^o\right)\)(3)

Xét tam giác MCA và tam giác ECB

có: AC=CB ( tam giác ABC đều)

\(\widehat{ACM}=\widehat{BCE}\)( theo (2))

\(\widehat{EBC}=\widehat{MAC}\)( theo (3))

=> Tam giác MCA =Tam giác ECB

=> CM=CE

=> tam giác MEC cân

Câu c) Trên nửa mặt phẳng bờ AM  không chứa điểm C dựng tam giác đều AMN

=> \(\widehat{AMN}=60^o\)

và NA=NM=AM

Ta có: \(\widehat{NAB}+\widehat{BAM}=\widehat{NAM}=60^o=\widehat{BAC}=\widehat{BAM}+\widehat{MAC}\)

=> \(\widehat{NAB}=\widehat{MAC}\)(1)

Xét tam giác NAB và tam giác MAC 

có: AB=AC ( tam giác ABC đều)
NA=AM ( tam giác AMN đều)

\(\widehat{NAB}=\widehat{MAC}\)( theo (1))

=> Tam giác NAB=MAC

=> NB=MC

Suy ra: MN:BM:NB=MA:MB:MC=3:4:5

=> Tam giác NMB vuông tại M

=> \(\widehat{NMB}=90^o\)

=> \(\widehat{AMB}=\widehat{AMN}+\widehat{NMB}=60^o+90^o=150^o\)

Em tham khảo nhé!

Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo link này nhé!

Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath

Phía nửa mặt phẳng bờ AB không chứa M lấy điểm N sao cho AMN là tam giác đều

Ta có ˆCAB=ˆMANCAB^=MAN^

<=>ˆCAM+ˆMAB=ˆMAB+ˆBANCAM^+MAB^=MAB^+BAN^

<=>ˆCAM=ˆBANCAM^=BAN^ (1)

mà CA =BA và AM =AN (2)

từ (1, 2) =>△CAM=△BAN△CAM=△BAN (c, g, c) (3)

(3) =>CM =BN

ta có MA2=MB2+MC2MA2=MB2+MC2

<=>MN2=MB2+BN2MN2=MB2+BN2

=>t giác MBN vuông tại B

(3) =>ˆACM=ˆABNACM^=ABN^

ˆMBN=ˆABM+ˆABN=90∘MBN^=ABM^+ABN^=90∘

<=>ˆABM+ˆACM=90∘ABM^+ACM^=90∘

<=>(60∘−ˆMBC)+(60∘−ˆMCB)=90∘(60∘−MBC^)+(60∘−MCB^)=90∘

<=>ˆMBC+ˆMCB=30∘MBC^+MCB^=30∘

<=>ˆBMC=180∘−30∘=150∘

thankinhachi