Chứng minh rằng với x >0 và x # 1 thì căn x phần căn x - 1 - 1 phần căn x - căn x = căn x + 1 phần căn x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
6 tháng 11 2019
a) \(A=x^2-2x+2=\left(x-1\right)^2+1>0\forall x\inℝ\)
b) \(x-x^2-3=-\left(x^2-x+3\right)\)
\(=-\left(x^2-x+\frac{1}{4}+\frac{11}{4}\right)\)
\(=-\left[\left(x-\frac{1}{2}\right)^2+\frac{11}{4}\right]\)
\(=-\left[\left(x-\frac{1}{2}\right)^2\right]-\frac{11}{4}\le\frac{-11}{4}< 0\forall x\inℝ\)
PT
2
PT
1
CM
16 tháng 8 2018
x ≤ 0 ⇒ |x| = -x
Suy ra: x + |x| = x – x = 0
Vậy mọi x ≤ 0 đều là nghiệm của phương trình x + |x| = 0
NT
3
11 tháng 8 2017
Ta có : x2 - 2xy + y2 + 1 = (x - y)2 + 1
Vì : \(\left(x-y\right)^2\ge0\forall x\in R\)
Nên : \(\left(x-y\right)^2+1\ge1\forall x\in R\)
Suy ra : \(\left(x-y\right)^2+1>0\forall x\in R\)
Vậy x2 - 2xy + y2 + 1 \(>0\forall x\in R\)
Ta có : x - x2 - 1
= -(x2 - x + 1)
\(=-\left(x^2-x+\frac{1}{4}+\frac{3}{4}\right)\)
\(=-\left(x^2-x+\frac{1}{4}\right)-\frac{3}{4}\)
\(=-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\)
Vì : \(-\left(x-\frac{1}{2}\right)^2\le0\forall x\in R\)
Nên : \(-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\le-\frac{3}{4}< 0\)
Vậy x - x2 - 1 \(< 0\forall x\in R\)
L
30 tháng 11 2016
- Biết a – b = 7 tính : A = a2(a + 1) – b2(b – 1) + ab – 3ab(a – b + 1)
- Cho ba số a, b, c khác 0 thỏa nãm đẳng thức :
LG
4
4 tháng 8 2016
ta có A=x2-2x+2=x2-2x+1+1=(x+1)2+1
ta thấy : (x+1)2\(\ge\)0 với mọi x
1>0
=> A=(x+1)2+1\(\ge\)1=> A\(\ge\)0
=> ĐPCM
A=(x+1)2+1\(\ge\)1 vơi smoij x
dấu = xảy ra khi x=-1
=> GTNN A=1 khi x=-1
=>
CM
8 tháng 1 2017
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
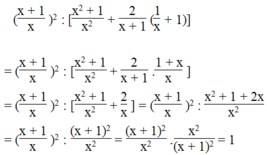
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.