Cho tam giác ABC nội tiếp (O) . M,N là 2 điểm thuộc cung nhỏ AC sao cho MN// AC và tia BM nằm giữa tia BA và tia BN . Bm giao AC tại P. Gọi Q là 1 điểm thuộc cung nhỏ BC sao cho PQ vuông góc với BC. QN giao AC tại R. F là giao điểm của AQ với BN. Chứng minh rằng AFB=BPQ+ABR
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


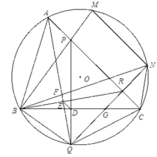
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q

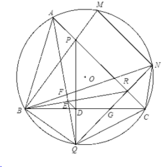
Ta có:
B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^