Đáp án B

Phương trình (1) có hai nghiệm dương phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt lớn hơn 1.

Bảng biến thiên của hàm số  y = t 2 - 10 t

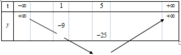
Phương trình (2) có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi -25< m < -9

Vậy S = {-24;-23;...;-10} và n(S) =15

Điều kiện xác định: x ≠ 0 .

Đặt  t = x + 1 x ⇒ t 2 − 2 = x 2 + 1 x 2 ≥ 2 ⇒ t ≥ 2 ⇔ t ≥ 2 t ≤ − 2

Phương trình đã cho trở thành  2 t 2 − 2 − 3 t − 2 m + 1 = 0

⇔ 2 t 2 − 3 t − 2 m − 3 = 0 ⇔ 2 t 2 − 3 t − 3 = 2 m      ( 1 )

Xét hàm số y = f ( t ) = 2 t 2 − 3 t − 3 có bảng biến thiên:

(1) Có nghiệm t thỏa mãn t ≥ 2 t ≤ − 2     k h i    2 m ≥ − 1 2 m ≥ 11 ⇔ m ≥ − 1 2 ⇒ S = − 1 2 ; + ∞

Vậy T = 3

Đáp án cần chọn là: D

Đặt x + 1 t = t , t ≥ 2  khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0    ( * )

Phương trình  2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn  t ≥ 2

Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m

Xét parabol  P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:

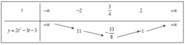
Từ bảng biến thiên ta có phương trình (*) có nghiệm  t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )  khi và chỉ khi  5 m ≥ - 1  hoặc  5 m ≥ 11

Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5

Đáp án cần chọn là: B

Lời giải:

Đặt tổng trên là $A$.

Với $n=1$ thì $2^n+3^n+4^n=9$ là scp (thỏa mãn)

Xét $n\geq 2$. Khi đó:

$2^n\equiv 0\pmod 4; 4^n\equiv 0\pmod 4$

$\Rightarrow A=2^n+3^n+4^n\equiv 3^n\equiv (-1)^n\pmod 4$

Vì 1 scp khi chia 4 chỉ có thể có dư là $0$ hoặc $1$ nên $n$ phải là số chẵn.

Đặt $n=2k$ với $k$ nguyên dương.

Khi đó: $A=2^{2k}+3^{2k}+4^{2k}\equiv (-1)^{2k}+0+1^{2k}\equiv 2\pmod 3$
Một scp khi chia 3 chỉ có thể có dư là 0 hoặc 1 nên việc chia 3 dư 2 như trên là vô lý

Vậy TH $n\geq 2$ không thỏa mãn. Tức là chỉ có 1 giá trị $n=1$ thỏa mãn.

Đáp án A

Nhận xét: Số giao điểm của C : y = f x  với Ox bằng số giao điểm của C ' : y = f x − 2017  với Ox

Vì m > 0  nên C ' ' : y = f x − 2017 + m  có được bằng cách tịnh tiến C ' : y = f x − 2017  lên trên m đơn vị

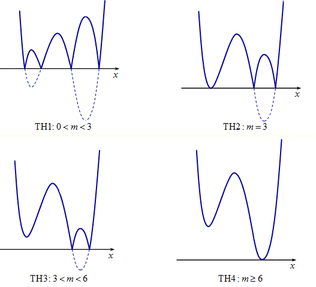
T H 1 : 0 < m < 3  Đồ thị hàm số có 7 điểm cực trị (loại)

T H 2 : m = 3  Đồ thị hàm số có 5 điểm cực trị (NHẬN)

T H 3 : 3 < m < 6  Đồ thị hàm số có 5 điểm cực trị (NHẬN)

T H 4 : m > 6  Đồ thị hàm số có 3 điểm cực trị (loại)

Vậy 3 ≤ m < 6.  Do m ∈ ℤ *  nên m ∈ 3 ; 4 ; 5  

Vậy tổng giá trị tất cả các phần tử của S bằng 12

 Đáp án A

Đồ thị hàm số y = f x có 3 điểm cực trị Đồ thị hàm số y = f x + 2018 có 3 điểm cực trị

Dựa vào ĐTHS y = f x ⇒ y = f x + 2018  có 7 điểm cực trị

Do đó, để hàm số y = f x + 2018 + 1 3 m 2  có 5 điểm cực trị khi và chỉ khi  3 ≤ 1 3 m 2 ≤ 6

Kết hợp với điều kiện m ∈ ℤ +  suy ra  m = 3 ; 4

Chú ý: Đồ thị hàm số y = f x + C  được cho bởi cách tịnh tiến đồ thị hàm số theo trục Oy C đơn vị

Chọn C

Sao lại bằng -3 được ạ? 

Chọn B

Đáp án là A