Cho đường tròn tâm (o), bán kính R=6cm, M là một điểm cách o 10cm. Tính độ dài tiếp tuyến kẻ từ M đến (o)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KD
25 tháng 4 2017
Dùng định lý Py-ta-go tính:
Tam giác OAB vuông tại B nên:
AB2 = OA2 – OB2 = 102 -62 =64
⇒ AB = 8
được AB=8cm.
13 tháng 10 2021
a: Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)
30 tháng 9 2021
Bài 2:
Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)
6 tháng 5 2021
\(=\sqrt{64}=8\left(cm\right)\)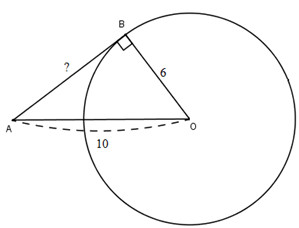
Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:
AB=\(\sqrt{AO^2-OB^2}=\sqrt{10^2-6^2}\)\(=\sqrt{64}=8\left(cm\right)\)
Đề này tương tự nên bạn nhìn rồi dựa vào làm nhá
Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB
Theo định lí Pitago trong tam giác vuông OAB có :
\(AB=\sqrt{AO^2-BO^2}=\sqrt{10^2-6^2}\)
\(=\sqrt{64}=8\left(cm\right)\)
Vậy : AB = 8cm