CHo đ/tr O bán kính R .Tử M nằm ngoài đ/tr kẻ 2 tiếp tuyến MA,MB .Qua A kẻ đường thẳng // MO cắt (O) tại E ,đường thẳng ME cắt (O) tại F (F khác E ) ,đường thẳng AF cắt MO tại N .Gọi H là Giao điểm của MO và AB .CMr : \(\frac{HB^2}{HF^2}-\frac{EF}{MF}=1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Chứng minh tứ giác MAOB nội tiếp đường tròn
Xét tứ giác MAOB có: \(\widehat{MAO}=90\text{°}\) (MA là tiếp tuyến của (O)); \(\widehat{MBO}=90\text{°}\) (MB là tiếp tuyến của (O))
→ \(\widehat{MAO}+\widehat{MBO}=180\text{°}\)
mà \(\widehat{MAO}\) và \(\widehat{MBO}\) là hai góc đối nhau
→ Tứ giác MAOB nội tiếp (dhnb) (đpcm)
b) Chứng minh MA.AB = 2MH.AO
Ta có: OA = OB (A, B ∈ (O))
→ O thuộc đường trung trực của AB (1)
Lại có: MA = MB (Tính chất hai tiếp tuyến cắt nhau)
→ M thuộc đường trung trực của AB (2)
Từ (1) và (2) → OM là đường trung trực của AB
→ OM ⊥ AB tại H và H là trung điểm của AB
→ \(\widehat{MHA}=90\text{°}\) và AB = 2AH
Xét ∆MAO và ∆MHA có: \(\widehat{MAO}=\widehat{MHA}=90\text{°}\); \(\widehat{M}\) chung
→ ∆MAO ∼ ∆MHA (g.g) → \(\dfrac{MA}{MH}=\dfrac{AO}{HA}\) (cặp cạnh tương ứng)
→ MA.HA = MH.AO
→ 2MA.HA = 2MH.AO
Mà AB = 2AH (cmt) → MA.AB = 2MH.AO (đpcm)
MA.HA = MH.AO
→ 2MA.HA = 2MH.AO
Mà AB = 2AH (cmt) → MA.AB = 2MH.AO (đpcm)
chỗ đây ko hiểu ;;;-;;;

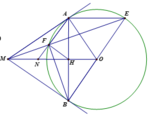
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn
Vẽ được các yếu tố để chứng minh phần (1).
Ta có M B O ^ = 90 0 , M A O ^ = 90 0 (theo t/c của tiếp tuyến và bán kính)
Suy ra: M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF. NA và MN = NH
Ta có A E / / M O ⇒ A E M ^ = E M N ^ mà A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^
Δ N M F v à Δ N A M có: M N A ^ chung; E M N ^ = M A F ^
nên Δ N M F đồng dạng với Δ N A M
⇒ N M N F = N A N M ⇒ N M 2 = N F . N A 1
Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N ^ h a y H B F ^ = F M H ^
=> MFHB là tứ giác nội tiếp
⇒ F H M ^ = F B M ^ = F A B ^ h a y F H N ^ = N A H ^
Xét Δ N H F & Δ N A H c ó A N H ^ c h u n g ; N H F ^ = N A H ^
=> Δ N M F đồng dạng Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A 2
Từ (1) và (2) ta có NH = HM
3) Chứng minh: H B 2 H F 2 − EF M F = 1 .
Xét Δ M AF và Δ M E A có: A M E ^ chung, M A F ^ = M E A ^
suy ra Δ M AF đồng dạng với Δ M E A
⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2 (3)
Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^ = B F H ^
Δ A E F và Δ H B F có: E F A ^ = B F H ^ ; F E A ^ = F B A ^
suy ra Δ A E F ~ Δ H B F
⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2 (4)
Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1

Ta có: \(\widehat{OAM}=\widehat{OBM}=90^o\)(Vì AM là đường trung tuyến của (O))
\(\Rightarrow\widehat{OAM}+\widehat{OBM}=180^o\)
=> Tứ giác MAOB nội tiếp
Theo tính chất tiếp tuyến cắt nhau ta có MA=MB; OA=OB
=> MO là đường trung trực của AB
=> MO _|_ AB tại H
Mà \(\widehat{BAE}=90^o\)hay AE _|_ AB. Do đó AE // MO
Vì AE // MO và MA là tiếp tuyến của (O) nên \(\widehat{NMF}=\widehat{AEF}=\widehat{NAM}\)
=> Tam giác NMA đồng dạng tam giác NFM (gg)
=> \(\frac{NM}{NF}=\frac{NA}{NM}\)\(\Rightarrow NM^2=AN\cdot NF\left(1\right)\)
Ta có: \(\widehat{MFB}=\widehat{MHB}=90^o\)=> Tứ giác MFHB nội tiếp
\(\Rightarrow\widehat{FHN}=\widehat{FBM}\)mà \(\widehat{FBM}=\widehat{NAH}\)
\(\Rightarrow\widehat{NAH}=\widehat{FHN}\)
\(\Rightarrow\Delta NAH\)đồng dạng \(\Delta NHF\left(g.g\right)\)
\(\Rightarrow\frac{NA}{NH}=\frac{NH}{NF}\Rightarrow NH^2=NA\cdot NF\left(2\right)\)
(1)(2) => NM2=NH2 => MN=NH (đpcm)

GƠI Ý PHẦN C: Như ý b ta có MN^2=NF.NA
bẠN HÃY CỐ ÉP NH^2=NF.NA . => ĐPCM.
( Chúc bạn học tốt , thân! <3 )

a) Ta có: \(\angle MAO+\angle MBO=90+90=180\Rightarrow MAOB\) nội tiếp
b) Vì \(MO\parallel AE\) \(\Rightarrow\angle NMF=\angle MEA=\angle MAF\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta NFM\) và \(\Delta NMA:\) Ta có: \(\left\{{}\begin{matrix}\angle NMF=\angle NAM\\\angle MNAchung\end{matrix}\right.\)
\(\Rightarrow\Delta NFM\sim\Delta NMA\left(g-g\right)\Rightarrow\dfrac{NF}{NM}=\dfrac{NM}{NA}\Rightarrow NM^2=NF.NA\)
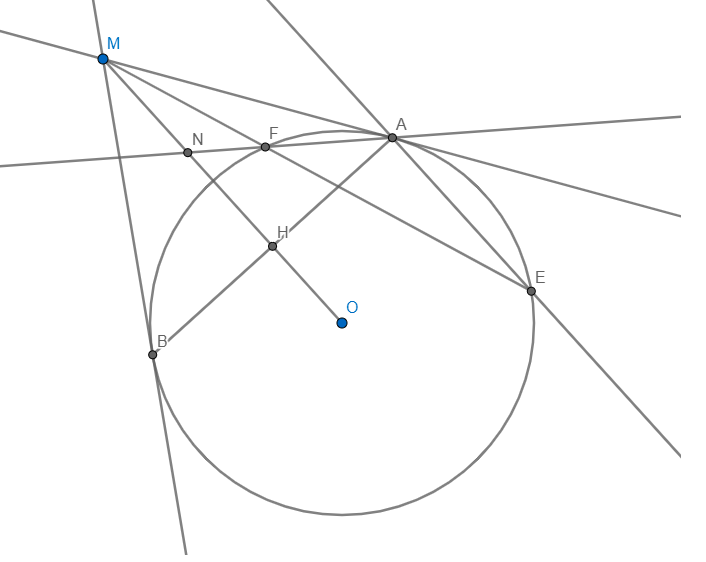
Ta có: AE // MO => ^AEM=^OME (So le trong) hay ^AEF=^HMF
Mà ^AEF=^FBH (=^FBA) (Cung chắn cung AF) => ^HMF=^FBH
=> Tứ giác MFHB nội tiếp đường tròn.
=> ^BFH=^BMH. Mà ^BMH=^ABO (Cùng phụ với ^MBH) => ^BFH=^ABO.
Dễ thấy MO vuông góc AB tại H, do AE//MO => AE vuông góc AB (Q/h song song, vg góc)
Ta thấy 3 điểm B;A;E cùng nằm trên (O) và ^BAE=900 => 3 điểm B;O;E thẳng hàng
=> ^ABO=^ABE. Do đó ^BFH=^ABE.
Lại có: ^ABE=^AFE (Cùng chắn cung AE) và ^AFE=^MFN (Đối đỉnh) => ^BFH=^MFN.
Xét \(\Delta\)FHB và \(\Delta\)FNM: ^BFH=^MFN; ^FBH=^FMN
=> \(\Delta\)FHB ~ \(\Delta\)FNM (g.g) => \(\frac{BH}{MN}=\frac{FH}{FN}\)(1)
^MFN + ^NFB = 900 => ^BFH + ^NFB = 900 => ^NFH = 900
=> \(\Delta\)NFH ~ \(\Delta\)HFA (g.g) => \(\frac{AH}{NH}=\frac{HF}{FN}\)(2)
Từ (1) và (2) => \(\frac{BH}{MN}=\frac{AH}{NH}\). Mà AH=BH => MN=NH, thay vào hệ thức:
\(\frac{HB}{MN}=\frac{HF}{NF}\Leftrightarrow\frac{HB}{HF}=\frac{MN}{NF}\)(Do \(\Delta\)BHF ~ \(\Delta\)MNF)
=> \(\frac{HB}{HF}=\frac{NH}{NF}\Leftrightarrow\frac{HB^2}{HF^2}=\frac{NH^2}{NF^2}\)
Áp dụng hệ quả ĐL Thales: \(\frac{EF}{MF}=\frac{AF}{NF}\)
\(\Rightarrow\frac{HB^2}{HF^2}-\frac{EF}{MF}=\frac{NH^2}{NF^2}-\frac{AF}{NF}=\frac{NH^2-AF.NF}{NF^2}\)
Dễ có: \(\Delta\)NFH ~ \(\Delta\)NHA => \(\frac{NF}{NH}=\frac{NH}{NA}\Rightarrow NH^2=NF.NA\)
\(\Rightarrow NH^2-AF.NF=NF.NA-AF.NF=NF.\left(NA-AF\right)=NF.NF=NF^2\)
\(\Rightarrow\frac{NH^2-AF.NF}{NF^2}=\frac{NF^2}{NF^2}=1\Rightarrow\)\(\frac{HB^2}{HF^2}-\frac{EF}{MF}=1.\)(đpcm).
Thank