Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, A = 3x2 + 18x + 33 => 3A = 9x2 + 54x + 99 = (3x)2 + 2.3x.9 + 81 + 18 = (3x + 9)2 + 18
Vì (3x + 9)2 > hoặc = 0 với mọi x => (3x + 9)2 + 18 luôn > 0 => 3A > o với mọi x hây > 0 với mọi x.
b, Ta có 3A = (3x + 9)2 + 18.
Vì (3x + 9)2 > hoặc = 0 với mọi x => (3x + 9)2 + 18 > hoặc = 18
Do đó 3A > hoặc = 18 => A > hoặc = 6.
Dấu = xảy ra <=> (3x + 9)2 = 0
<=> 3(x + 3) = 0
<=> x + 3 = 0
<=> x = -3
Vậy GTNN của A = 6 khi x = -3

Ta thay x bằng số -4. Khi đó -4+4=0, mà 0 mũ 2020 thì vẫn bằng 0. 0+17=17. Đáp án: 17

Điều kiện x ≠ 2 và x ≠ 0
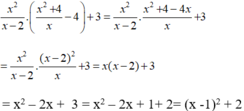
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)

a)Áp dụng BĐT bunhiacoxki ta có: \(\left(a^2+b^2\right)\left(1^2+1^2\right)\ge\left(a.1+b.1\right)^2=\left(a+b\right)^2=3^2=9\)
=>\(2\left(a^2+b^2\right)\ge9\Leftrightarrow a^2+b^2\ge\frac{9}{2}\)
Dấu "=" xảy ra khi: a=b
Vậy GTNN của N là 9/2 tại a=b
b)Ta có: \(a^2+b^2\ge\frac{9}{2}\) (câu a)
<=>(a+b)2-2ab\(\ge\frac{9}{2}\)
<=>\(9-2ab\ge\frac{9}{2}\)
<=>\(2ab\le\frac{9}{2}\)
<=>\(ab\ge\frac{9}{4}\)
<=>\(ab+2\le\frac{17}{4}\)
Dấu "=" xảy ra khi a=b
Vậy GTLN của P là 17/4 tại a=b
\(A=a+\frac{2}{a^2}=\frac{1}{2}a+\frac{1}{2}a+\frac{2}{a^2}\ge3\sqrt[3]{\frac{1}{2}a.\frac{1}{2}a.\frac{2}{a^2}}=3\sqrt[3]{\frac{1}{2}}\)
Dấu \(=\)khi \(\frac{1}{2}a=\frac{2}{a^2}\Leftrightarrow a=\sqrt[3]{4}\).