Cho hai đường tròn tâm O và O' tiếp xúc ngoài nhau tại A. Kẻ tiếp tuyến chung ngoài của hai đường tròn (B, C là tiếp điểm; \(B\in\left(O\right);C\in\left(O'\right)\)). Tiếp tuyến chung của hai đườn tròn tại A cắt BC tại M. AB cắt OM tại N, AC cắt O'M tại P. Chứng minh:a, M là trung điểm BCb, tứ giác MNAP là hình chữ nhậtc, MN . MO = MP . MO'd, Cho OA = 16cm, O'A = 9cm. Tính BCe, Giả sử BC cắt OO' tại E. Cho OA =...
Đọc tiếp
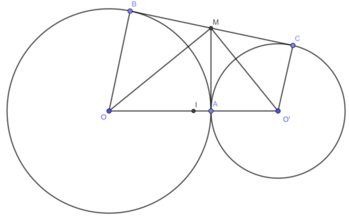
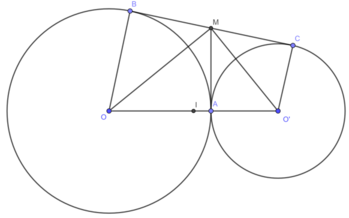
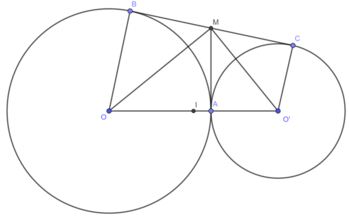
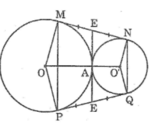
Cho hai đường tròn tâm O và O' tiếp xúc ngoài nhau tại A. Kẻ tiếp tuyến chung ngoài của hai đường tròn (B, C là tiếp điểm; \(B\in\left(O\right);C\in\left(O'\right)\)). Tiếp tuyến chung của hai đườn tròn tại A cắt BC tại M. AB cắt OM tại N, AC cắt O'M tại P. Chứng minh:
a, M là trung điểm BC
b, tứ giác MNAP là hình chữ nhật
c, MN . MO = MP . MO'
d, Cho OA = 16cm, O'A = 9cm. Tính BC
e, Giả sử BC cắt OO' tại E. Cho OA = 16cm, O'A = 9cm. Tính chu vi tam giác OCE
f, Đường thẳng OO' cắt đường tròn (O) và (O') lần lượt tại D, F ( \(D\ne A;F\ne A\)). DB cắt FC tại K. Chứng minh 3 điểm A, M, K thẳng hàng.
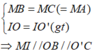
Mừng quá. Xong hết rồi. Hơn nửa tiếng bây giờ cũng được đền đáp =))
a) MB = MC (=MA) (giao điểm 2 tiếp tuyến cách đều tiếp điểm)
b) MA = MB = MC => T/g ABC vuông tại A => ^A = 90
T/g OAB cân tại O, có OM là đ/phân giác nên OM cũng là đ cao hay ^ANM = 90
Tương tự, ^APM = 90
=> đpcm
c) MO'/MO = O'C/BM (CMO' ~ BOM) = O'C/CM = CP/MP (CMO' ~ PMC) = MN/MP (PMC = NBM góc vuông - cạnh huyền - góc nhọn so le trong)
=> đpcm
d) Trong t/g vuông OMO' có MA là đường cao, OM^2 = OA.OO' <=> OM = 20 => BM = 12 (Pytago) => BC = 24
e) Dùng ta lét tìm ra OE, EC, còn OC tìm theo pytago trong t/g vuông OBC
f) ABKC là hình chữ nhật => AK cắt BC tại trung điểm M => đpcm