trên đoạn thẳng AB lấy một điểm M ( MA<MB) . Trên cùng một nửa mặt phẳng bờ là AB, vẽ tam giác đều AMC và BMD. Gọi E. F, I , K lần lượt là trung điểm của CM , CB , DM, DA . C/m EFIK là hình thang cân và KF= 1/2 CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
a:Vì AB<AM
nên B nằm giữa A và M
=>AB+BM=AM
=>BM=6cm
b: Vì B nằm giữa A và M
và BA=BM
nên B là trung điểm của AM
H
3 tháng 4 2023
`a,` Vì `AB=6cm;AM=12cm` mà `B` nằm giữa `AM`
`-> BM=AM-AB`
`->BM= 12-6`
`->BM=6cm`
Vậy `BM=6cm`
`b, B` là trung điểm của đoạn thẳng `MA` vì :
\(\left\{{}\begin{matrix}AB=BM=6cm\left(cmt\right)\\AB=BM=\dfrac{AM}{2}\end{matrix}\right.\)
`=>B` là trung điểm của đoạn thẳng `MA`
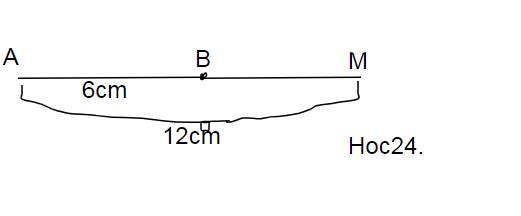
Vẽ không đẹp lắm ạ .
TD
3 tháng 4 2023
a,vì AM>AB
Nên điểm B nằm giữa 2 đoạn thảng AM
⇒độ dài đoạn thẳng BM=AM-AB
=12-6=6cm
b, Vì AB=BM=\(\dfrac{AM}{2}\)
Nên AB=BM=6cm
⇒ĐIểm B là trung điểm đoạn thẳng AM
7 tháng 12 2021
b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE
3 tháng 2 2019
B1) Tỉ số của AB=11( vì 7+4)
Tỉ số của MA/AB=7/11
TỈ SỐ AB/MB= 11/4
B2) Độ dài đoạn AB= 10:2=5
Độ dài đoạn MB =10-5
k nhá
4 tháng 2 2019
B1: Ta có: Tỉ số của AB là 11 ( = tỉ số MA + tỉ số MB)
=> tỉ số của MA/AB=7/11
tỉ số của AB/MB=11/4
B2: Độ dài của MA: 10/(2+3).2=4 cm
=> MB=AB-MA=10-4=6 cm
Chúc e hc tốt
19 tháng 8 2019
H là trung điểm AB nên AH = BH
d vuông góc với AB \(\Rightarrow\widehat{MHA}=\widehat{MHB}=90^o\)
Xét tam giác AHM và tam giác BHM có :
AH = HB
\(\widehat{MHA}=\widehat{HBM}=90^o\)
MH là cạnh chung
\(\Rightarrow\Delta AHM=\Delta MHB\)
\(\Rightarrow MA=MB\)
Chúc bạn học tốt !!!
8 tháng 11 2019
xét tam giác amh và tam giác bmh có
ah = hb (gt)
góc ahm = góc bhm (=90 độ)
mh chung
=> tam giác amh = tam giác bmh (c.g.c)
26 tháng 12 2023
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Ta có: ΔMAB=ΔMEC
=>AB=EC
Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
c: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
d: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)
nên \(\widehat{KME}+\widehat{IME}=180^0\)
=>I,M,K thẳng hàng
7jhjjjjhbn