Trên đồ thị (C):\(y=\frac{x-1}{x+2}\)có hau điểm mà tiếp tuyến tại các điểm đó đều song song với đường thẳng (d):\(3x-y+15=0\). Tìm tổng S các tung độ tiếp điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:Sửa đề: y=x^3-3x^2+2
y'=3x^2-3*2x=3x^2-6x
y=2
=>x^3-3x^2=0
=>x=0 hoặc x=3
=>y'=0 hoặc y'=3*3^2-6*3=27-18=9
A(0;2); y'=0; y=2
Phương trình tiếp tuyến có dạng là;
y-2=0(x-0)
=>y=2
A(3;2); y'=9; y=2
Phương trình tiếp tuyến có dạng là:
y-2=9(x-3)
=>y=9x-27+2=9x-25
b: Tiếp tuyến tại M song song với y=6x+1
=>y'=6
=>3x^2-6x=6
=>x^2-2x=2
=>x=1+căn 3 hoặc x=1-căn 3
=>y=0 hoặc y=0
M(1+căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1-căn 3)=6x-6-6căn3
M(1-căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1+căn 3)
=>y=6x-6+6căn 3

TXĐ: ![]() .
.
Ta có: 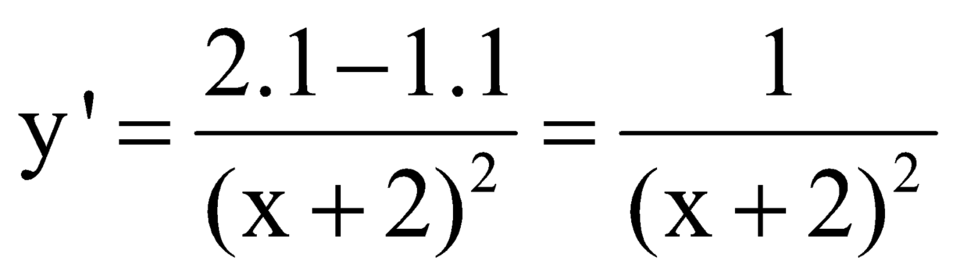
Gọi 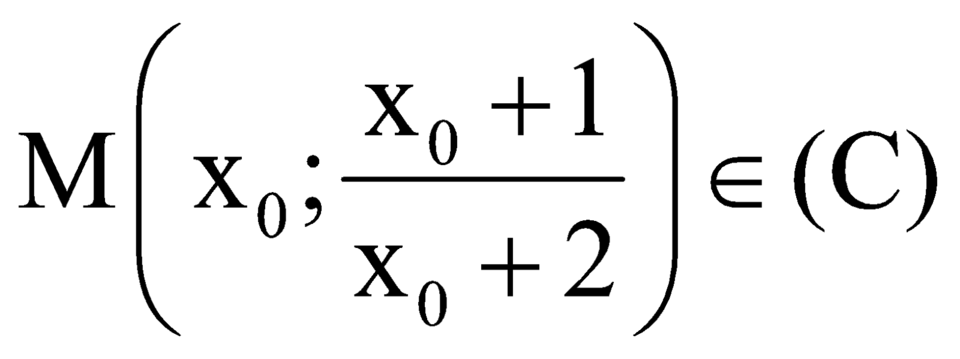
Ta có phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ ![]() là:
là:
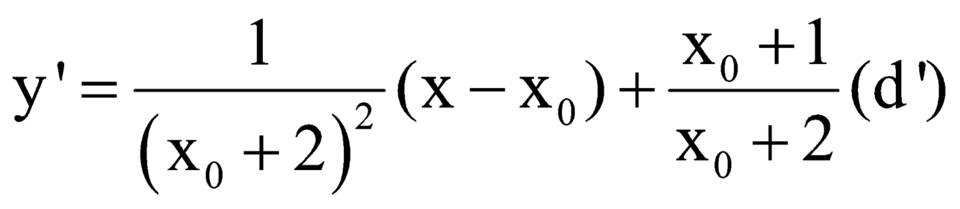
Để ![]() (vô nghiệm)
(vô nghiệm)
![]() Không có điểm M nào thỏa mãn yêu cầu bài toán.
Không có điểm M nào thỏa mãn yêu cầu bài toán.
Chọn A.
Chú ý: Phải đưa phương trình đường thẳng (d) về dạng ![]() và xác định hệ số góc của đường thẳng d cho chính xác, tránh sai lầm khi cho hệ số góc của đường thẳng d trong bài toán này bằng 1
và xác định hệ số góc của đường thẳng d cho chính xác, tránh sai lầm khi cho hệ số góc của đường thẳng d trong bài toán này bằng 1

Đáp án D.
y ' = 3 x 2 − 12 x + 9
Gọi M x 0 ; x 0 3 − 6 x 0 2 + 9 x 0 − 1 là một điểm bất kì thuộc (C) . Tiếp tuyến tại M:
y = 3 x 0 2 − 12 x 0 + 9 x − x 0 + x 0 3 − 6 x 0 2 + 9 x 0 − 1
⇔ y = 3 x 0 2 − 12 x 0 + 9 x − 2 x 0 3 + 6 x 0 2 − 1
Gọi A a ; a − 1 là một điểm bất kì thuộc đường thẳng y = x − 1 .
Tiếp tuyến tại M đi qua A ⇔ 3 x 0 2 − 12 x 0 + 9 a − 2 x 0 3 + 6 x 0 2 − 1 = a − 1
⇔
3
x
0
2
−
12
x
0
+
8
a
=
2
x
0
3
−
6
x
0
2
(*).
Từ A kẻ được hai tiếp tuyến đến C ⇔ * có hai nghiệm phân biệt.
Ta có
3 x 0 2 − 12 x 0 + 8 = 0 ⇔ x 0 = 6 ± 2 3 3
Dễ thấy x 0 = 6 ± 2 3 3 không thỏa mãn .
Với x 0 ≠ 6 ± 2 3 3 thì * ⇔ a = 2 x 0 3 − 6 x 0 2 3 x 0 2 − 12 x 0 + 8 .
Xét hàm số f x = 2 x 3 − 6 x 2 3 x 2 − 12 x + 8 . Ta có f ' x = 6 x 4 − 8 x 3 + 20 x 2 − 16 x 3 x 2 − 12 x + 8 2 .
Bảng biến thiên của :
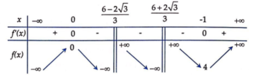
Vậy để (*) có 2 nghiệm phân biệt thì a ∈ 0 ; 4 . Suy ra tập T = 0 ; − 1 , 4 ; 3
Do đó tổng tung độ các điểm thuộc T bằng 2.



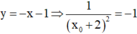


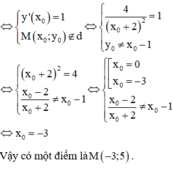
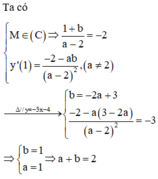


Gọi \(x_0\) là hoành độ của điểm thuộc (C) mà tại đó tiếp xuyến của (C) song song với (d)
Ta có \(y'\left(x_0\right)=\frac{3}{\left(x_0+2\right)^2}\), hệ số góc của \(\left(d\right):3x-y+15=0\) là 3
Suy ra \(\frac{3}{\left(x_0+2\right)^2}=3\Leftrightarrow\orbr{\begin{cases}x_0+2=1\\x_0+2=-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x_0=-1\\x_0=-3\end{cases}}\)
Hai điểm cần tìm là \(A\left(-1;-2\right),B\left(-3;4\right)\). Vậy \(S=-2+4=2.\)