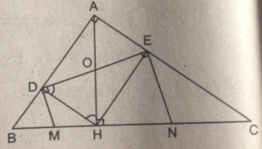
Cho tam giác ABC vuông tại B, đường cao BH . Cho biết AB cm AC cm 6 , 10 .
a) Tính độ dài các đoạn thẳng BC BH HA HC , , , .
b) Gọi M và N theo thứ tự là hình chiếu của H trên AB và BC. Chứng minh: BN BC BM BA . . .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng hệ thức giữa cạnh và đường cao trong các tam giác vuông

∆AHC và ∆AHB ta có:
AE.AC = A H 2 = AD.AB => ∆AHC ~ ∆AHB(c.g.c)
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ∆ABC tính được AH = 3cm => DE = 3cm
Trong ∆AHB vuông ta có:
tan A B C ^ = A H H B => A B C ^ ≈ 56 0 , S A D E = 27 13 c m 2

b: Xét ΔBHA vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(BM\cdot BA=BH^2\left(1\right)\)
Xét ΔBHC vuông tại H có HN là đường cao ứng với cạnh huyền CB
nên \(BN\cdot BC=BH^2\left(2\right)\)
Từ (1) và (2) suy ra \(BM\cdot BA=BH\cdot BC\)

Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà 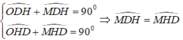
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.