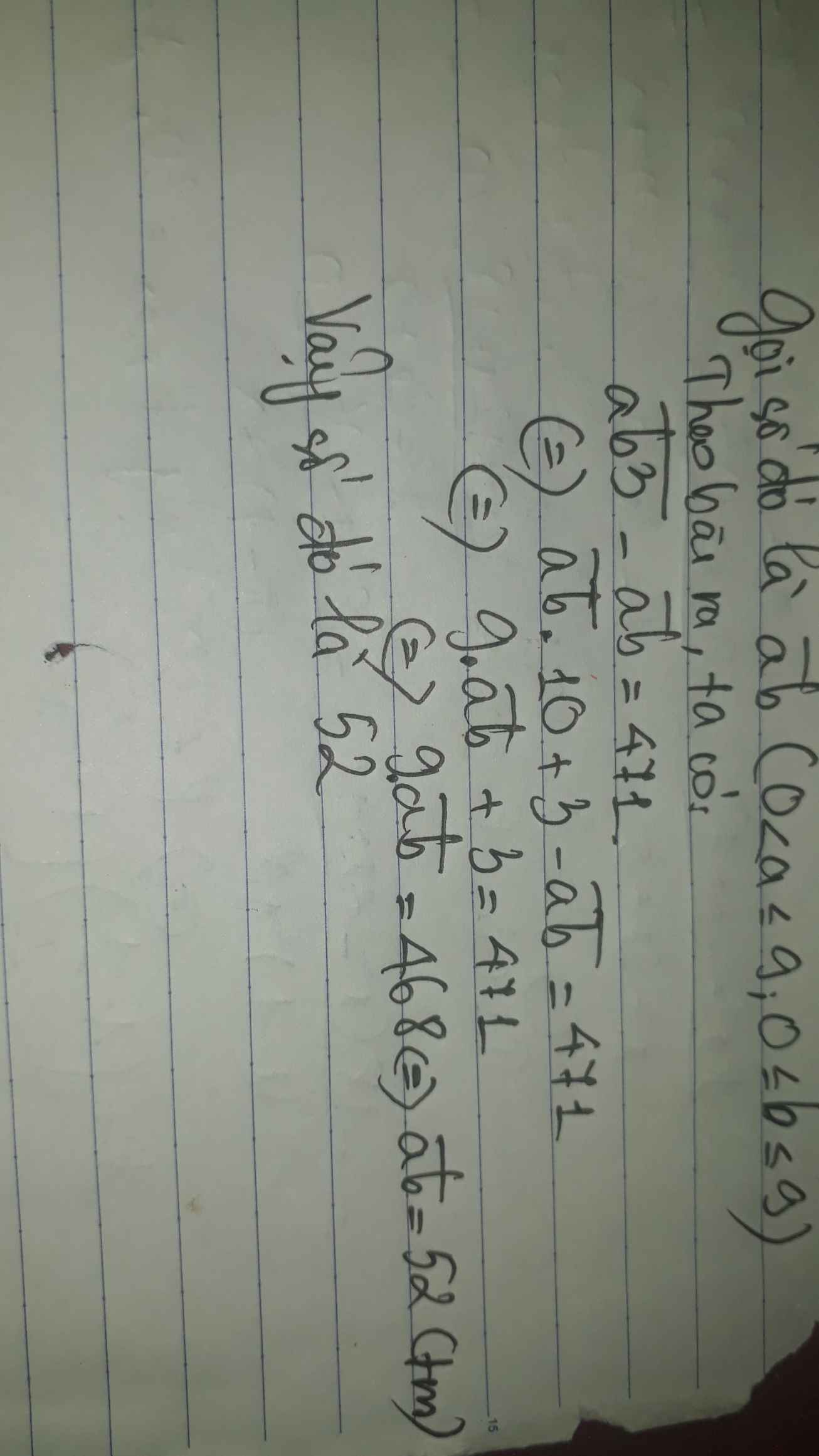hai chữ số viết thêm là 0 và 6

20 nhe

Giải :

Gọi hai chữ số đó là x và y. Số cũ là ab. Ta có :

abxy = ab + 1960

ab . 100 + xy = ab + 1960

 ab . 99 + xy = 1960

Vì ab, xy < 100 nên ab phải bằng 19

1881 + xy = 1960

=> xy = 79

Vậy 2 chữ số viết thêm là 7 và 9. Sỗ chẵn cần tìm là 19

1986 mà bn

Lời giải:
Gọi số cần tìm là $\overline{ab}$. Ta có:
$\overline{ab2}=405+\overline{ab}$

$\overline{ab}\times 10+2=405+\overline{ab}$

$\overline{ab}\times 10-\overline{ab}=405-2$

$\overline{ab}\times 9=403$

$\overline{ab}=403:9$ không phải số tự nhiên. 

Đề có vẻ sai. Bạn xem lại.

 Gọi số có 2 chữ số cần tìm là ab và 2 chữ số viết thêm là c, d. 
Theo đề bài ta có: abcd - ab = 1986. Ta có thể sắp bài toán lại như sau: 
abcd 
-- ab 
------- 
1986 
Qua bài toán trên ta thấy a chỉ có thể là 1 hoặc 2 

* a = 1, ta có: 
1bcd 
-- 1b 
------- 
1986 
Xét vị trí hàng chục của bài toán trên thì c chỉ có thể là 0 hoặc 9 
** c = 0 
1b0d 
-- 1b 
------- 
1986 
Xét vị trí hàng trăm ta có b = 0, ta có: 
100d 
-- 10 
------- 
1986 
Xét hàng đơn vị ta có d = 6, bài toán: 
1006 
-- 10 
------- 
1986 
Vị trí hàng chục của bài toán không phù hợp (loại) 

** c = 9 
1b9d 
-- 1b 
------- 
1986 
Suy ra b = 9, ta có: 
199d 
-- 19 
------- 
1986 
Xét vị trí hàng đơn vị: d - 9 = 6 thì phải giữ 1 nhưng vị trí hàng chục không phù hợp (loại) 
Vậy a không thể bằng 1 
* Xét trường hợp a = 2, ta có: 
2bcd 
-- 1b 
------- 
1986 
Từ đây ta có: b = 0 và bài toán: 
20cd 
-- 20 
------- 
1986 
Ta có d = 6 và c = 0, bài toán: 
2006 
-- 20 
------- 
1986 
Vậy số cần tìm là 20 và 2 chữ số thêm vào là 0,6

Cho một​ số có hai chữ số.Nếu viết thêm hai chữ số nữa vào bên phải số đó thì được một số mới lớn hơn số đã cho 1986 đơn vị.Hãy tìm số đã cho và hai chữ số mới được viết thêm.

 Gọi số có 2 chữ số cần tìm là ab và 2 chữ số viết thêm là c, d. 
Theo đề bài ta có: abcd - ab = 1986. Ta có thể sắp bài toán lại như sau: 
abcd 
-- ab 
------- 
1986 
Qua bài toán trên ta thấy a chỉ có thể là 1 hoặc 2 

* a = 1, ta có: 
1bcd 
-- 1b 
------- 
1986 
Xét vị trí hàng chục của bài toán trên thì c chỉ có thể là 0 hoặc 9 
** c = 0 
1b0d 
-- 1b 
------- 
1986 
Xét vị trí hàng trăm ta có b = 0, ta có: 
100d 
-- 10 
------- 
1986 
Xét hàng đơn vị ta có d = 6, bài toán: 
1006 
-- 10 
------- 
1986 
Vị trí hàng chục của bài toán không phù hợp (loại) 

** c = 9 
1b9d 
-- 1b 
------- 
1986 
Suy ra b = 9, ta có: 
199d 
-- 19 
------- 
1986 
Xét vị trí hàng đơn vị: d - 9 = 6 thì phải giữ 1 nhưng vị trí hàng chục không phù hợp (loại) 
Vậy a không thể bằng 1 
* Xét trường hợp a = 2, ta có: 
2bcd 
-- 1b 
------- 
1986 
Từ đây ta có: b = 0 và bài toán: 
20cd 
-- 20 
------- 
1986 
Ta có d = 6 và c = 0, bài toán: 
2006 
-- 20 
------- 
1986 
Vậy số cần tìm là 20 và 2 chữ số thêm vào là 0,6

 nhé !

Số có hai chữ số có dạng: \(\overline{ab}\) 

Khi viết thêm vào bên phải số đó hai chữ số: c;d

Thì được số mới có dạng: \(\overline{abcd}\)

Theo bài ra ta có: \(\overline{abcd}\) - \(\overline{ab}\) = 1995

                            \(\overline{ab}\) \(\times\) 100 + \(\overline{cd}\) - \(\overline{ab}\) = 1995

                            \(\overline{ab}\) \(\times\) ( 100 - 1) + \(\overline{cd}\) = 1995

                            \(\overline{ab}\) \(\times\) 99 + \(\overline{cd}\)         = 1995

                           \(\overline{ab}\) \(\times\) 99 = 1995 - \(\overline{cd}\)

                           \(\overline{ab}\)        = \(\dfrac{1995-\overline{cd}}{99}\) 

                           \(\overline{ab}\)   = 20 - \(\dfrac{cd-15}{99}\)

                          ⇒ \(\overline{cd}\) - 15 ⋮ 99  vì \(\overline{cd}\) ≤ 99 ⇒ \(\overline{cd}\)  = 15; 

                           \(\overline{ab}\) = 20

Vậy số có hai chữ số ban đầu là 20; hai chữ số viết thêm là: 15

Lời giải:
Gọi số cần tìm là $\overline{ab}$. Điều kiện: $a,b$ là số tự nhiên; $a,b\leq 9; a\neq 0$

Theo bài ra ta có:

$\overline{ab3}-\overline{ab}=471$

$\overline{ab}\times 10+3-\overline{ab}=471$

$\overline{ab}\times (10-1)+3=471$

$\overline{ab}\times 9+3=471$

$\overline{ab}\times 9=468$

$\overline{ab}=468:9=52$
Vậy số cần tìm là $52$