Cho hình chóp sabc có SA vuông góc với mặt phẳng (abc) là tam giác vuông tại B, bc=2a. Khoảng cách từ C đến mặt phẳng (sab) bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
2 tháng 8 2017
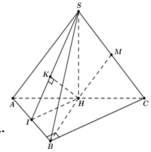
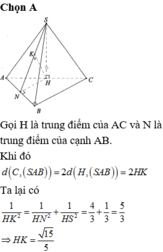
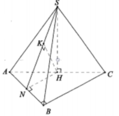
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

CM
22 tháng 2 2018
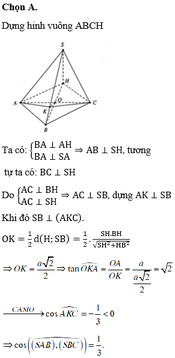
Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
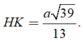
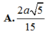
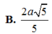
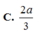
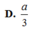
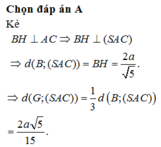
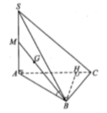
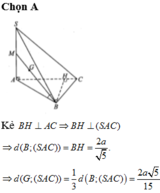
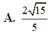

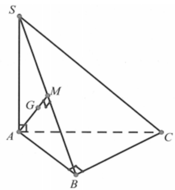
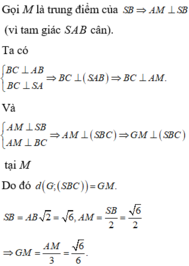
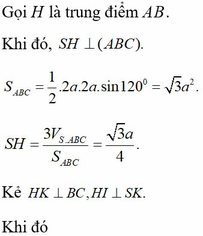
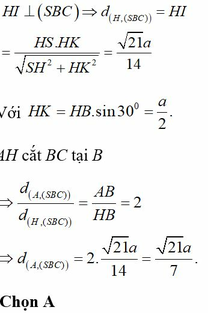
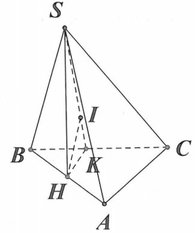
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=2a\)