Giải giúp em câu 12 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a,
c, Gọi \(\left(D_3\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=-2;b\ne0\\3x+3=ax+b,\forall x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\-a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-2\end{matrix}\right.\)
Vậy \(\left(D_3\right):y=-2x-2\)

12 I consider that to manage to know what other people are thinking is quite impossible

a: \(=\dfrac{\left(x+1\right)\left(2x-1\right)+x^2-3x^2}{x\left(2x-1\right)}\)
\(=\dfrac{2x^2-x+2x-1+\left(-2x^2\right)}{x\left(2x-1\right)}\)
\(=\dfrac{x-1}{x\left(2x-1\right)}\)
b: Để B=0 thì x-1=0
=>x=1



Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.


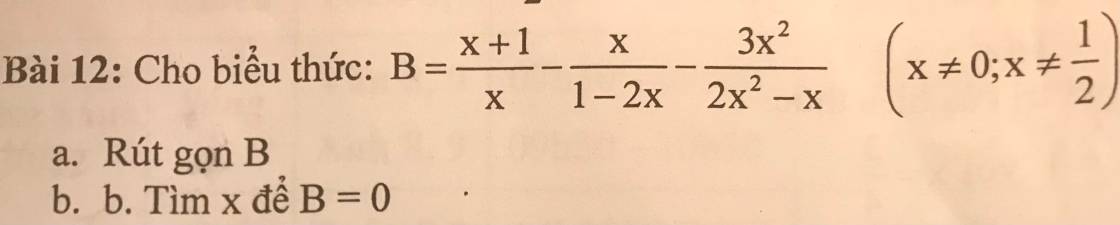



Gọi N là trung điểm AB, P là trung điểm BC
\(\dfrac{SH}{SN}=\dfrac{SK}{SP}=\dfrac{2}{3}\) (t/c trọng tâm) \(\Rightarrow HK||NP\) , mà \(NP||AC\) (đường trung bình) \(\Rightarrow HK||AC\)
\(\Rightarrow\) Giao tuyến của (IHK) và (ABC) là 1 đường thẳng song song AC
Trong mp (SNI), nối IH cắt MN tại F
Qua F kẻ đường thẳng song song AC lần lượt cắt AB tại Q và BC tại G
\(\Rightarrow QG=\left(IHK\right)\cap\left(ABC\right)\)
b.
S nằm trên IM, N nằm trên SH nên \(MN\in\left(IHM\right)\)
\(\Rightarrow\) (IHM) và (SBC) chứa 2 đường thẳng song song NM và BC (MN là đường trung bình tam giác ABC)
\(\Rightarrow\) Giao tuyến của (IHM) và (SBC) là 1 đường thẳng song song BC
Do S là 1 điểm chung của 2 mp, qua S kẻ đường thẳng d song song BC
\(\Rightarrow d=\left(IHM\right)\cap\left(SBC\right)\)