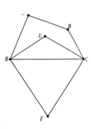
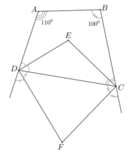
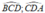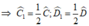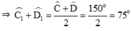Cho tứ giác ABCD có các tia phân giác của góc A và D vuông góc với nhau tại E
a) Tứ giác ABCD là hình gì? Chứng minh
b) Các tia phân giác của các góc B và C cắt nhau tại F. Các tia phân giác của các góc ngoài đỉnh A và D cắt nhau tại M. Các tia phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Chứng minh 4 điểm M,N,E,F thẳng hàng
c) Cho biết AB = a, BC = b, CD = c, DA= d (a,b,c,d có cùng đơn vị độ dài). CMR: Nếu a+c=b+d thì E trùng với F
Giúp em với ạ, vẽ hình giúp em nhé. Cảm ơn mn ạ