Bài 1:Một người đi xe đạp từ A đến B trong thời gian đã định, khi còn cách B là 30km người ấy nhận thấy rằng sẽ đến B chậm 30' nếu giữ nguyên vận tốc cũ.Do đó,người đó tăng vận tốc thêm 5km/h và đến B sớm hơn 30' so với dự định. Tính vận tốc lúc đầu của người đi xe đạp.Bài 2:Một bè nứa trôi tự do và một cano đồng thời rời bến A để xuôi dòng.Cano xuôi dòng được 96km thì quay ngay trở...
Đọc tiếp
Bài 1:Một người đi xe đạp từ A đến B trong thời gian đã định, khi còn cách B là 30km người ấy nhận thấy rằng sẽ đến B chậm 30' nếu giữ nguyên vận tốc cũ.Do đó,người đó tăng vận tốc thêm 5km/h và đến B sớm hơn 30' so với dự định. Tính vận tốc lúc đầu của người đi xe đạp.
Bài 2:Một bè nứa trôi tự do và một cano đồng thời rời bến A để xuôi dòng.Cano xuôi dòng được 96km thì quay ngay trở về A,thời gian cả đi lẫn về hết 14h.Trên đường quay trở về A,khi còn cách A 24km thì cano gặp bè nứa trôi nói trên.Tính vận tốc riêng cano và vận tốc dòng nước.
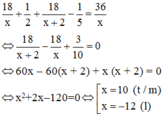
Bài 1:
Gọi vận tốc ban đầu là $a$ km/h
Thời gian đi quãng đường $30$ km còn lại với vận tốc cũ: $t_1=\frac{30}{a}$ (giờ)
Thời gian đi quãng đường 30 km còn lại với vận tốc mới: $t_2=\frac{30}{a+5}$ (giờ)
Theo bài ra thì: $t_1-t_2=1$ giờ
$\Leftrightarrow \frac{30}{a}-\frac{30}{a+5}=1$
$\Rightarrow a=10$ (km/h)
Thời gi
Bài 2:
Gọi vận tốc riêng của cano là $a$ km/h và vận tốc dòng nước là $b$ km/h
ĐK: $a>b$
Theo bài ra ta có:
\(\left\{\begin{matrix} \frac{96}{a-b}+\frac{96}{a+b}=14\\ \frac{24}{b}=\frac{96}{a+b}+\frac{96-24}{a-b}\end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} \frac{96}{a-b}+\frac{96}{a+b}=14\\ \frac{96}{a+b}+\frac{72}{a-b}=\frac{24}{b}\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 192a=14(a-b)(a+b)\\ 24a=14b(a-b)\end{matrix}\right.\)(*)
\(\Rightarrow 8.14b(a-b)=14(a-b)(a+b)\)
\(\Leftrightarrow 8b=a+b\Leftrightarrow a=7b\). Thay vô 1 trong 2 pt trong $(*)$ thì:
$24.7b=14b.6b$
$168b=84b^2$
$b=2$ (km/h)
$a=7b=14$ (km/h)