Giúp mik giải bài 4 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài V:
-ĐKXĐ: \(x\ne\pm1\).
\(\dfrac{m}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2}{x^2-1}\)
\(\Leftrightarrow\dfrac{m\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow mx+m+x^2-x=x^2\)
\(\Leftrightarrow m\left(x+1\right)=x\)
\(\Leftrightarrow m=\dfrac{x}{x+1}\)
-Vì m,x nguyên:
\(\Rightarrow x⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1-1\right)⋮\left(x+1\right)\)
\(\Rightarrow-1⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{0;-2\right\}\) (nhận)
*\(x=0\Rightarrow m=\dfrac{x}{x+1}=\dfrac{0}{0+1}=0\)
\(x=-2\Rightarrow m=\dfrac{x}{x+1}=\dfrac{-2}{-2+1}=1\)
-Vậy với \(m=0\) thì \(S=\left\{0\right\}\)
với \(m=1\) thì \(S=\left\{-2\right\}\)

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

Bài cuối mình không thấy rõ đề nhưng mình đoán là thế này bạn nhé.
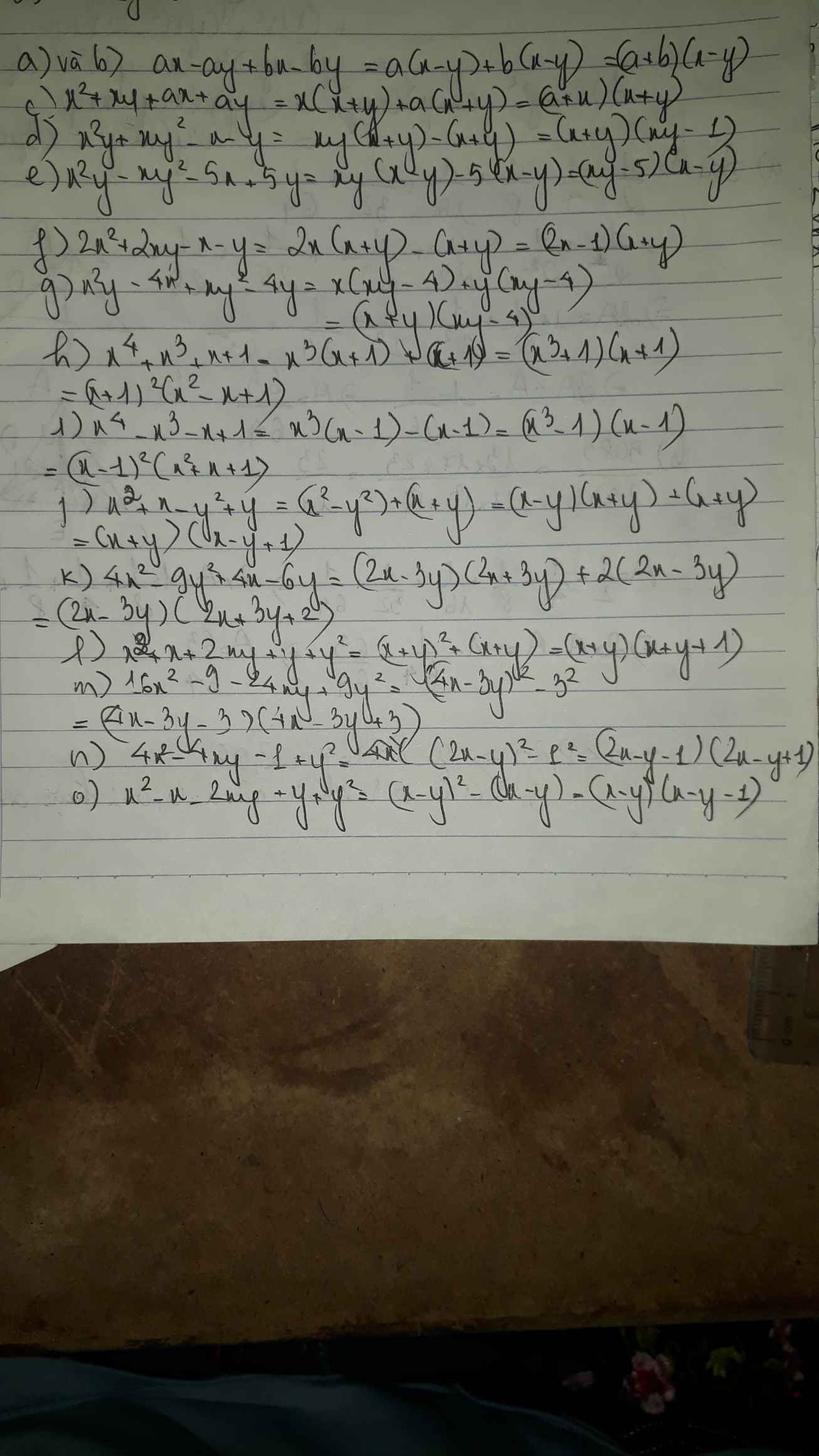

Câu 3:
a: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
b: Ta có: \(2x\left(x+7\right)-3x\left(x+1\right)\)
\(=2x^2+14x-3x^2-3x\)
\(=-x^2+11x\)
Câu 2:
a: Ta có: \(\left(-8x^5+12x^3-16x^2\right):4x^2\)
\(=-8x^5:4x^2+12x^3:4x^2-16x^2:4x^2\)
\(=-2x^3+3x-4\)
b: Ta có: \(\left(12x^3y^3-18x^2y+9xy^2\right):6xy\)
\(=12x^3y^3:6xy-18x^2y:6xy+9xy^2:6xy\)
\(=2x^2y^2-3x+\dfrac{3}{2}y\)
c: Ta có: \(\dfrac{x^3-11x^2+27x-9}{x-3}\)
\(=\dfrac{x^3-3x^2-8x^2+24x+3x-9}{x-3}\)
\(=x^2-8x+3\)
d: Ta có: \(\dfrac{6x^4-13x^3+7x^2-x-5}{3x+1}\)
\(=\dfrac{6x^4+2x^3-15x^3-5x^2+12x^2+4x-5x-\dfrac{5}{3}-\dfrac{10}{3}}{3x+1}\)
\(=2x^3-5x^2+4x-\dfrac{5}{3}-\dfrac{\dfrac{10}{3}}{3x+1}\)

\(\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)=1\)
\(\Leftrightarrow\left(-2+x^2\right)^5=1\)
\(\Leftrightarrow-2+x^2=1\)
\(\Leftrightarrow x^2=3\Leftrightarrow x=\pm\sqrt{3}\)

Bài 1:
a: Ta có: \(3\left(x-\dfrac{1}{2}\right)-3\left(x-\dfrac{1}{3}\right)=x\)
\(\Leftrightarrow x=3x-\dfrac{3}{2}-3x+1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
b: Ta có: \(-\dfrac{4}{3}\left(x-\dfrac{1}{4}\right)=\dfrac{3}{2}\left(2x-1\right)\)
\(\Leftrightarrow x\cdot\dfrac{-4}{3}+\dfrac{1}{3}-3x+\dfrac{3}{2}=0\)
\(\Leftrightarrow x\cdot\dfrac{-13}{3}=-\dfrac{11}{6}\)
hay \(x=\dfrac{11}{26}\)

Câu 3 :
Số mol của sắt
nFe = \(\dfrac{m_{Fe}}{M_{Fe}}=\dfrac{5,6}{56}=0,1\left(mol\right)\)
Pt : Fe + H2SO4 → FeSO4 + H2\(|\)
1 1 1 1
0,1 0,1 0,1 0,1
a) Số mol của khí hidro
nH2 = \(\dfrac{0,1.1}{1}=0,1\left(mol\right)\)
Thể tích của khí hidro ở dktc
VH2 = nH2 . 22,4
= 0,1 . 22,4
= 2,24 (l)
b) Số mol của muối sắt (II) sunfat
nFeSO4 = \(\dfrac{0,1.1}{1}=0,1\left(mol\right)\)
Khối lượng của muối sắt (II) sunfat
mFeSO4 = nFeSO4 . MFeSO4
= 0,1 . 152
= 15,2 (g)
c) Số mol của dung dịch axit sunfuric
nH2SO4 = \(\dfrac{0,1.1}{1}=0,1\left(mol\right)\)
200ml = 0,2l
Nồng độ mol của dung dịch axit sunfuric
CMH2SO4 = \(\dfrac{n}{V}=\dfrac{0,1}{0,2}=0,5\left(M\right)\)
Chúc bạn học tốt
Câu 4 :
Số mol của photpho
nP = \(\dfrac{m_P}{M_P}=\dfrac{6,2}{31}=0,2\left(mol\right)\)
Pt : 4P + 5O2 → (to) 2P2O5
4 5 2
0,2 0,25 0,1
a) Số mol của đi photpho pentaoxit
nP2O5 = \(\dfrac{0,2.2}{4}=0,1\left(mol\right)\)
Khối lượng của đi photpho pentaoxit
mP2O5 = nP2O5 . MP2O5
= 0,1 . 142
= 14,2 (g)
b) Số mol của khí oxi
nO2 = \(\dfrac{0,2.5}{4}=0,25\left(mol\right)\)
Thể tích của khí oxi ở dktc
VO2 = nO2 . 22,4
= 0,25 . 22,4
= 5,6 (l)
c) Pt : CH4 + 2O2 → CO2 + 2H2O\(|\)
1 2 1 2
0,25 0,125
Số mol của khí cacbonic
nCO2 = \(\dfrac{0,25.1}{2}=0,125\left(mol\right)\)
Thể tích của khí cacbonic ở dktc
VCO2 = nCO2 . 22,4
= 0,125 . 22,4
= 2,8 (l)
Chúc bạn học tốt





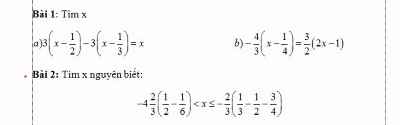 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ
a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=15^2-9^2=144\)
hay AH=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{12^2}{9}=16\left(cm\right)\)