Cho hình thang cân ABCD có đáy AB song song với CD và AB < CD.
a) Gọi I là giao điểm của hai đường chéo hình thang ABCD. Chứng minh
IA = IB, IC = ID.
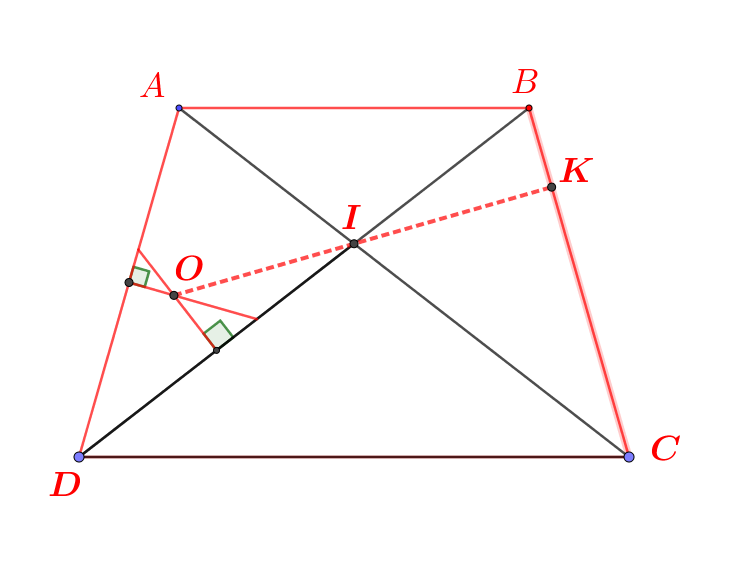
b) Tia DA và tia CB cắt nhau tại O. Chứng minh OI vừa là đường trung
trực của đoạn AB vừa là đường trung trực của đoạn CD.
c) Tính các góc của hình thang ABCD nếu góc ABC - ADC = 180 độ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔADE vuông tại E và ΔBCF vuông tại F có
AD=BC(ABCD là hình thang cân)
\(\widehat{ADE}=\widehat{BCF}\)(ABCD là hình thang cân)
Do đó: ΔADE=ΔBCF(Cạnh huyền-góc nhọn)
Suy ra: DE=CF(Hai cạnh tương ứng)
b) Xét ΔADB và ΔBCA có
AD=BC(ABCD là hình thang cân)
AB chung
DB=CA(ABCD là hình thang cân)
Do đó: ΔADB=ΔBCA(c-c-c)
Suy ra: \(\widehat{DBA}=\widehat{CAB}\)(hai góc tương ứng)
hay \(\widehat{IAB}=\widehat{IBA}\)
Xét ΔIAB có \(\widehat{IAB}=\widehat{IBA}\)(cmt)
nên ΔIAB cân tại I(Định lí đảo của tam giác cân)
Suy ra: IA=IB
c) Ta có: \(\widehat{OAB}=\widehat{ODC}\)(hai góc đồng vị, AB//CD)
\(\widehat{OBA}=\widehat{OCD}\)(hai góc đồng vị, AB//CD)
mà \(\widehat{ODC}=\widehat{OCD}\)(ABCD là hình thang cân)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)(cmt)
nên ΔOAB cân tại O(Định lí đảo của tam giác cân)
Suy ra: OA=OB
Ta có: OA+AD=OD(A nằm giữa O và D)
OB+BC=OC(B nằm giữa O và C)
mà OA=OB(cmt)
và AD=BC(ABCD là hình thang cân)
nên OD=OC
Ta có: IA+IC=AC(I nằm giữa A và C)
IB+ID=BD(I nằm giữa B và D)
mà IA=IB(cmt)
và AC=BD(cmt)
nên IC=ID
Ta có: OA=OB(cmt)
nên O nằm trên đường trung trực của AB(1)
Ta có: IA=IB(cmt)
nên I nằm trên đường trung trực của AB(2)
Ta có: OD=OC(cmt)
nên O nằm trên đường trung trực của DC(3)
Ta có: ID=IC(cmt)
nên I nằm trên đường trung trực của DC(4)
Từ (1) và (2) suy ra OI là đường trung trực của AB
Từ (3) và (4) suy ra OI là đường trung trực của DC

a) Xét \(\Delta\)ADE và \(\Delta\)BCF :
AED^ = BFC^ =90o
AD = BC
ADE^ = BCF^
=> \(\Delta\)ADE = \(\Delta\)BCF (cạnh huyền_góc nhọn)
=> DE = CF (2 cạnh tương ứng)
b) Xét \(\Delta\)DAB và \(\Delta\)CBA:
AD= BC
DAB^ = CBA^
AB chung
=> \(\Delta\)DAB = \(\Delta\)CBA (c.g.c)
=> ADB^ =BCA^ (2 góc tương ứng)
Ta có: ADC^ = ADB^ + BDC^ => BDC^ = ADC^ - ADB^
BCD^ = BCA^ + ACD^ => ACD^ = BCD^ - BCA^
mà ADC^ = BCD^ và ADB^ = BCA^ (cmt)
=> BDC^ = ACD^
=> \(\Delta\)DIC cân tại I
=> ID = IC
Xét \(\Delta\)AID và \(\Delta\)BIC:
AD = BC
ADI^ = BCI^ (cmt)
ID = IC (cmt)
=> \(\Delta\)AID = \(\Delta\)BIC (c.g.c)
=> IA = IB (2 cạnh tương ứng)
c)
d)
---ko làm nữa đâu--- +.+

2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.

a: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{IDC}=\widehat{ICD}\)
Xét ΔIDC có \(\widehat{IDC}=\widehat{ICD}\)
nên ΔIDC cân tại I


help