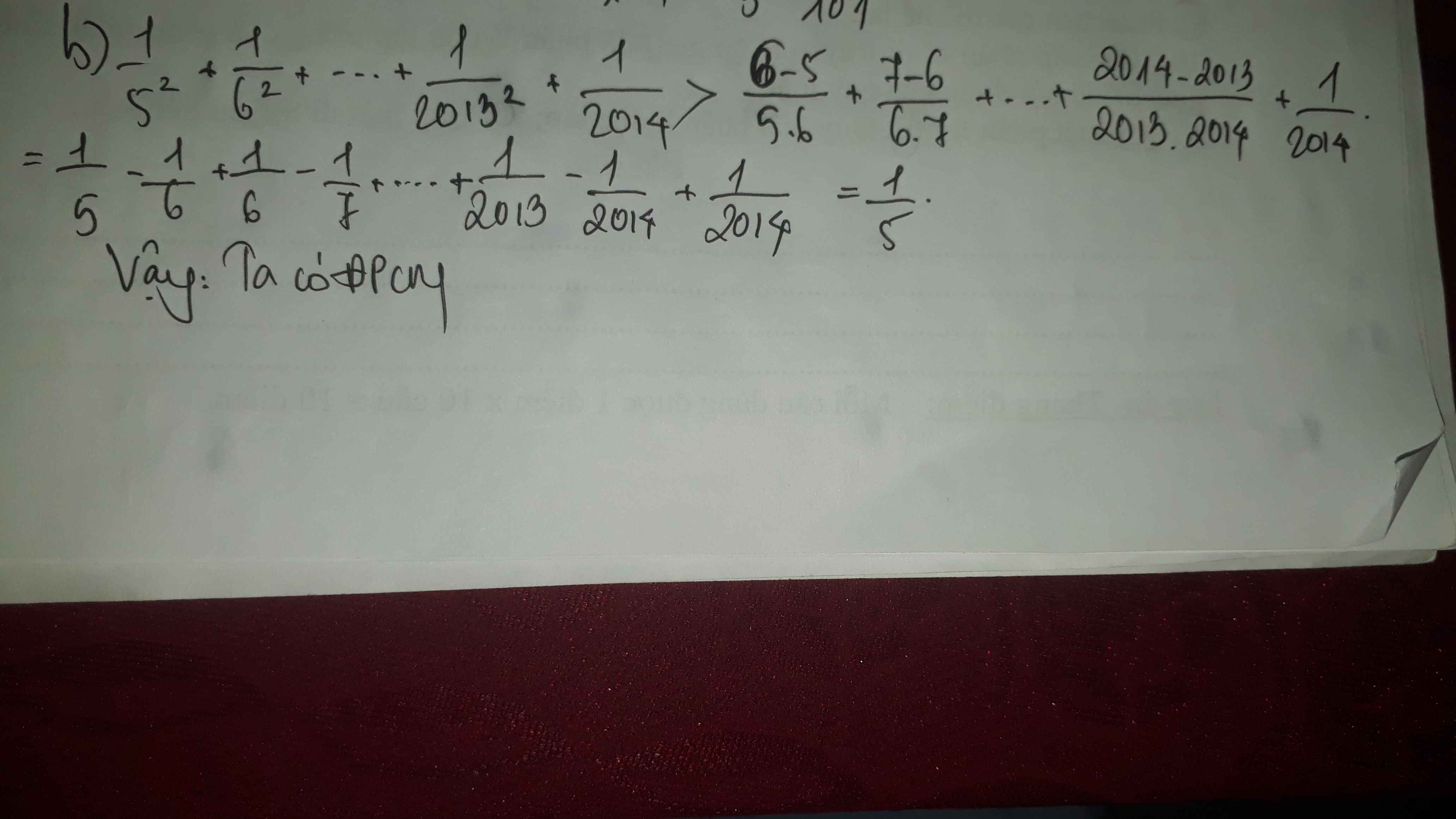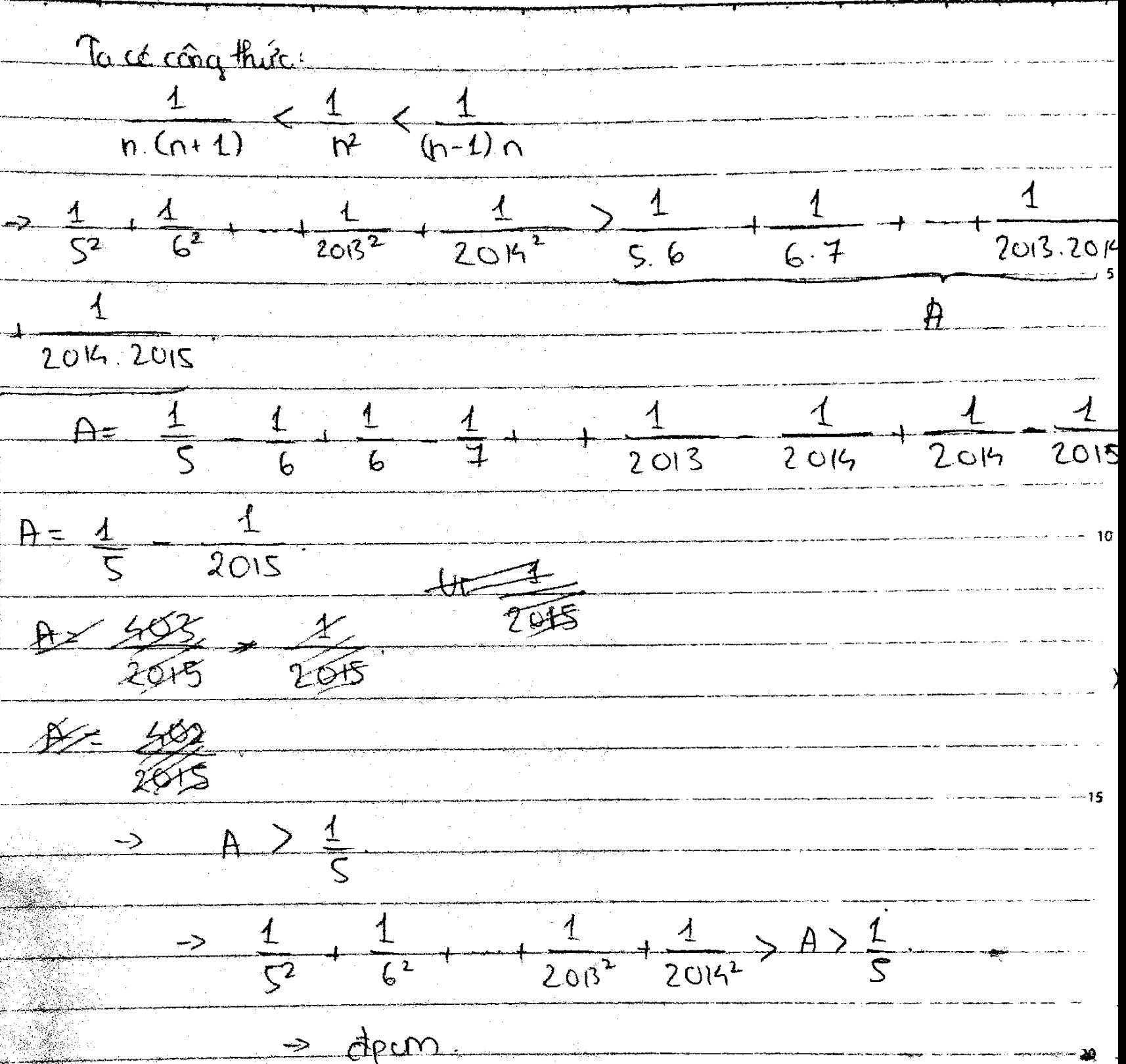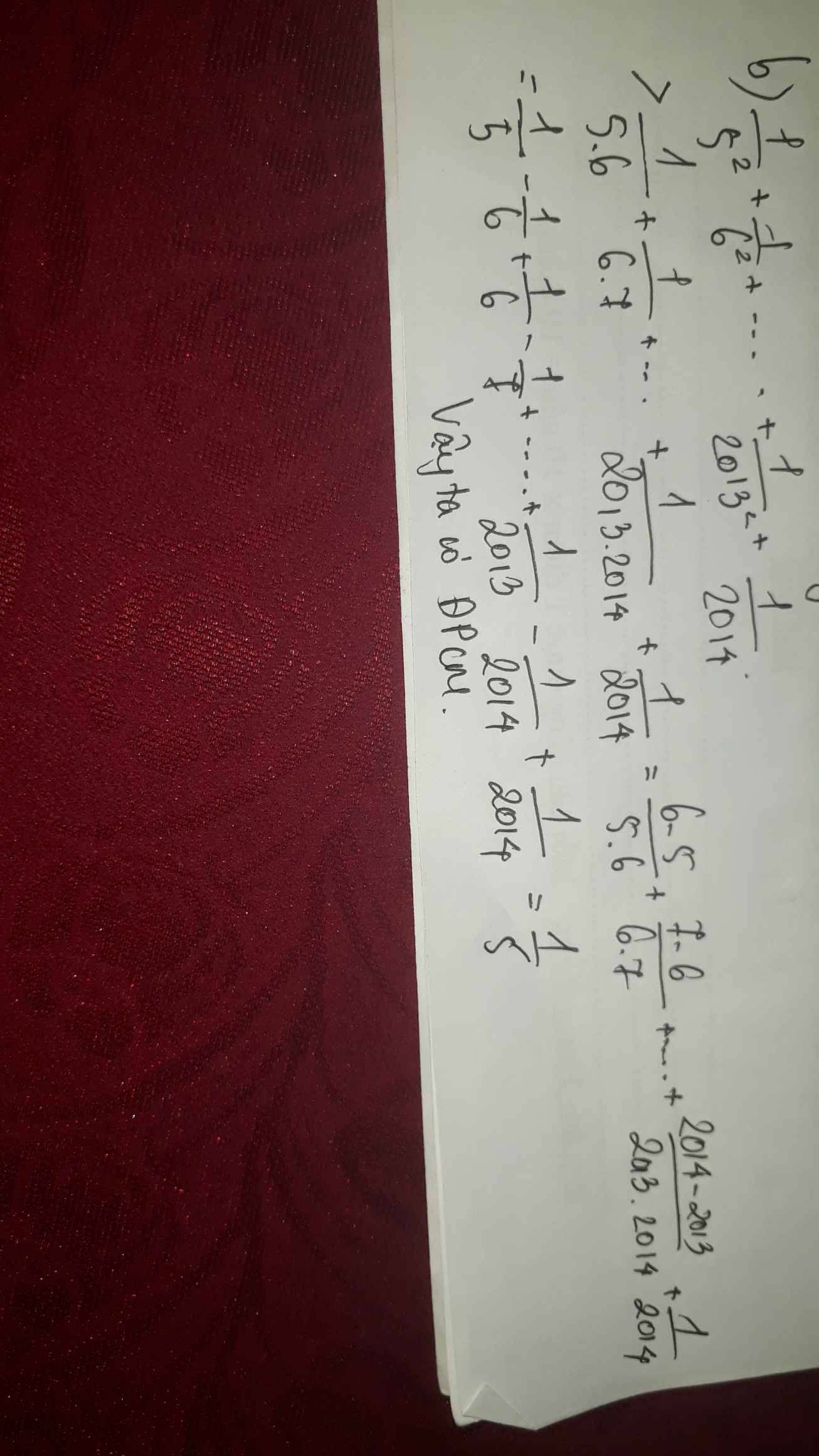chứng minh rằng :
a) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\) b)\(\dfrac{1}{5^2}+\dfrac{1}{6^5}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014}>\dfrac{1}{5}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
Đặt \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2014^2}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{2014.2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{150}=\dfrac{1}{5}\) (đpcm)
TG
11 tháng 4 2022
1/4^2 + 1/5^2 +... + 1/100^2 < 1/3.4 + 1/4.5 +...+ 1/99.100
A=1/3 - 1/4 + 1/4 - 1/5 +...+ 1/99 - 1/100
=1/3 - 1/100 < 1/3
NP
2
6 tháng 9 2021
\(\dfrac{1}{5^2}< \dfrac{1}{4.5}\)
\(\dfrac{1}{6^2}< \dfrac{1}{5.6}\)
......
\(\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(\Rightarrow\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{99.100}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\)
6 tháng 9 2021
Ta có: \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\)
NT
10 tháng 2 2018
\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+....+\dfrac{1}{100^2}\\ >\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{100.101}\\ =\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{101}\\ =\dfrac{1}{5}-\dfrac{1}{101}\\ =\dfrac{96}{505}\\ >\dfrac{1}{6}\)
\(\dfrac{1}{5^2}+...+\dfrac{1}{100^2}\\ < \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+....+\dfrac{1}{99.100}\\ =\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\)
NN
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
Đặt \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
Ta có: \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{99.100}\)
\(\Rightarrow A< \dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(\Rightarrow A< \dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\) (đpcm)
25 tháng 4 2023
A=1/3^2+1/4^2+1/5^2+1/6^2+...+1/100^2<1/2-1/3+1/3-1/4+...+1/99-1/100
=>A<1/2-1/100<1/2