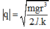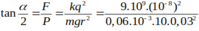Hai quả cầu nhỏ giống nhau, cùng khối lượng 𝑚 = \(0,4\sqrt{3}\) g, mang điện tích 𝑞 = \(4.10^{-8}\)C được treo tại cùng một điểm bằng hai sợi dây mảnh. Do lực đẩy tĩnh điện hai quả cầu tách ra xa nhau một đoạn 𝑎 = 6 cm. Cho 𝑔 = 10 \(m\)/\(s^2\). Xác định góc của các sợi dây so với phương thẳng đứng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Góc lệch \(\alpha\) của dây treo được xác định bằng hệ thức (suy từ điều kiện cân bằng của hai quả cầu :)
\(\tan\alpha=\frac{F_đ}{P}\)
Với \(F_đ=k\frac{q^2}{a^2}\) Như vậy \(\tan\alpha=\frac{kq^2}{mga^2}\)
Thay số ta được : \(\tan\alpha=1\) suy ra \(\alpha=45^o\)
mình chưa hiểu đoạn tan a = F/P lắm bạn giải thích lại hộ mình đc ko

Đáp án C.
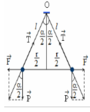
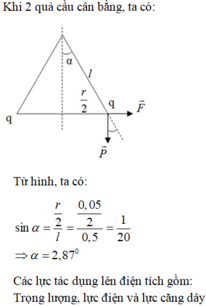
Khi hệ cân bằng:
sin α = 0 , 5 r ℓ → α = 30 0 tan α = F m g = k q 2 m g r 2 ⇒ q = m g r 2 tan α k
⇒ q = 0 , 2 . 10 . 0 , 05 2 tan 2 , 866 0 9 . 10 9 = 5 , 66 . 10 - 6 C
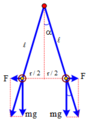

Đáp án: A
Ở vị trí cân bằng mỗi quả cầu sẽ chịu tác dụng của ba lực: trọng lực
P
→
, lực tĩnh điện
F
→
và lực căng dây
T
→
. Khi đó: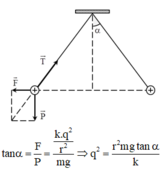
Vì r rất nhỏ so với ℓ nên α nhỏ
Ta có  do vậy độ lớn của điện tích đã truyền cho quả cầu là:
do vậy độ lớn của điện tích đã truyền cho quả cầu là: