đặt điện áp xoay chiều u=U căn 2 coswt vào hai đầu đoạn mạch RLC mắc nối tiếp trong đó tụ điện C có điện dung thay đổi được. khi C=Co thì điện áp hiệu dụng giữa hai bản tụ đạt giá trị cực đại và điện áp hiệu dụng giữa hai đầu điện trở R là 75V. khi đó vào thời điểm điện áp tức thời giữa hai đầu đoạn mạch là 75 căn 6 thì điện áp tức thời giữa hai đầu đoạn mạc RL...
Đọc tiếp
đặt điện áp xoay chiều u=U căn 2 coswt vào hai đầu đoạn mạch RLC mắc nối tiếp trong đó tụ điện C có điện dung thay đổi được. khi C=Co thì điện áp hiệu dụng giữa hai bản tụ đạt giá trị cực đại và điện áp hiệu dụng giữa hai đầu điện trở R là 75V. khi đó vào thời điểm điện áp tức thời giữa hai đầu đoạn mạch là 75 căn 6 thì điện áp tức thời giữa hai đầu đoạn mạc RL là 25 căn 6V. điện áp hiệu dụng giữa hai đầu đoạn mạch là
A.75 căn 6 B.75 căn 3 C.150 D.150 căn 2
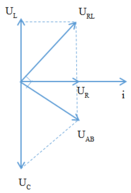
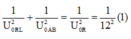
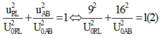
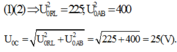
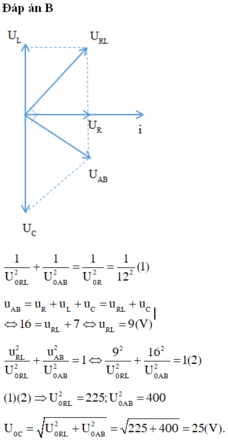
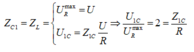
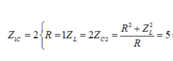
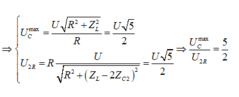
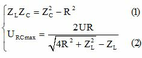
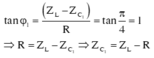
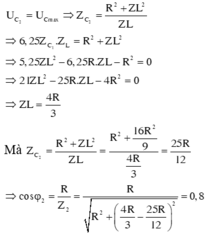
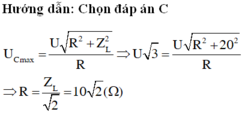
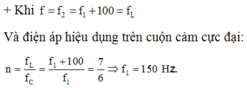
C thay đổi để UC max thì uRL vuông pha với u mạch.
Từ giản đồ véc tơ ta có: \(\frac{1}{U_R^2}=\frac{1}{U_{RL}^2}+\frac{1}{U_m^2}=\frac{1}{75^2}\left(1\right)\)
Do sự vuông pha nên: \(\left(\frac{u_{RL}}{U_{0RL}}\right)^2+\left(\frac{u_m}{U_{0m}}\right)^2=1\Rightarrow\left(\frac{25\sqrt{6}}{U_{0RL}}\right)^2+\left(\frac{75\sqrt{6}}{U_{0m}}\right)^2=1\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình, giải ra ta được: \(U_{0m}=300V\)
\(\Rightarrow U_m=150\sqrt{2}V\)
Đáp án D.